算数｢点の移動・図形の移動｣［中学受験］
ツカム先生もくり返しアドバイスしているとおり、この単元の攻略（こうりゃく）のポイントは、問題を読んで自分で実際に図をかいてみることです。問題に示された「点」や「図形」が、どのように動き、新たにどのような線や図形をえがくのか、慣れていくほど正確な図をかくことができるようになり、答えを導き出すプロセスが楽しく感じられるようになるはずです。今回もツカム先生と楽しく勉強していきましょう。
■算数｢点の移動・図形の移動｣
こんにちは、合格総理大臣ミスター・ツカムです。
今回は「点の移動・図形の移動」を取り上げます。この単元を苦手にしている人は多いと思います。アタマの中でいろいろと想像しなくちゃいけないからね。初めはイメージしにくいけれど、何度も練習をくり返すと絶対にわかるようになりますから。心配しないで一つひとつ自分のものにしていきましょう。
「点の移動」には、動物がおりの周りをぐるっと回ったりするときの問題や、四角形の辺の上を点が移動していく問題があります。
「図形の移動」には、図形どうしが重なってはなれたりする問題、図形の周りを別の図形が回転していったりする問題があります。
より早く定着させるには、類似の問題を解いて理解を深めることです。では、いっしょにがんばりましょう。
| 問題1 |
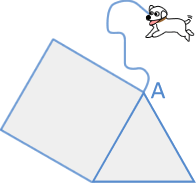 右の図のような、1辺が6mの正方形と正三角形を合わせた形をした花壇（かだん）があり、犬がAのところから長さ9mの綱（つな）でつながれています。花壇の周りには柵（さく）があり、この犬は花壇の外を動きまわることができますが花壇の中には入れません。 犬が動くことのできる範囲（はんい）の面積を求めなさい。 ただし、円周率は3.14として計算しなさい。 （浦和明の星女子中 2007年 第2回） |
| ＜問題1の考え方と答え＞ |
| まずは、点の移動の基本的な問題ですね。 犬が移動できる範囲（はんい）の図を正確にかくことができたら、それでOKです。 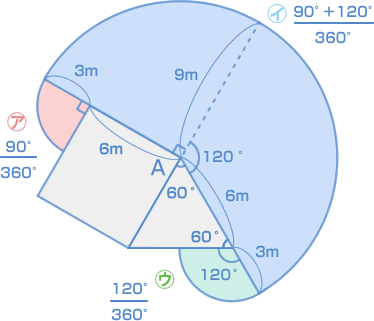  3つ別々に計算して合計してもいいのですが、計算の工夫でスムーズにできそうなので、式を1つにまとめてみますよ。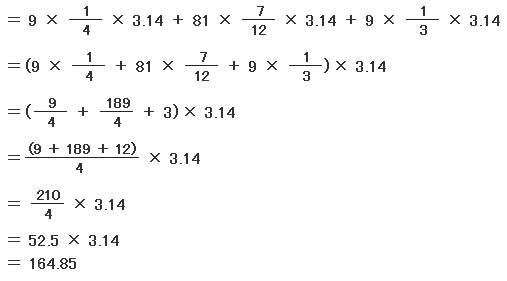    
|
| 問題2 |
| 図1の台形ABCDの辺上を点Pが毎秒3cm の速さでA→B→C→Dの順に動きます。図２のグラフは点Pの動いた時間と三角形APDの面積の関係を表しています。 （1）ADの長さは何cmですか。 （2）台形ABCDの面積は何cm² ですか。 （3）三角形APDの面積が台形ABCDの面積の半分になるのは、点Pが点Aを出発してから何秒後と何秒後ですか。 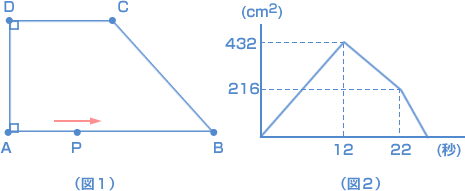 （和洋九段女子中 2007年 3回） |
| ＜問題2 （1）の考え方と答え＞ |
点Pの動きによって、三角形APDの面積がどのように変化するかを考えましょう。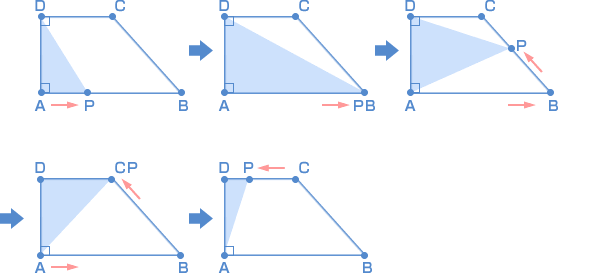 点Pが辺AB上を動くとき、面積は大きくなります。 点Pが辺BC上を動くとき、面積は小さくなります。 点Pが辺CD上を動くとき、面積はさらに小さくなります。 つまり、図2のグラフで点PがA、B、C、Dに着いたときは、次のようになります。 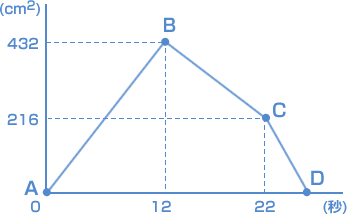 点PがBに着いたときのAPの長さは、毎秒3cmで12秒移動したから、 3 × 12 ＝ 36（cm） そのときの三角形の面積は 432cm² だから、 ADの長さを □ とすると、 □ × 36 ÷ 2 ＝ 432 □ × 18 ＝ 432 □ ＝ 432 ÷ 18 □ ＝ 24  |
| ＜問題2 （2）の考え方と答え＞ |
台形に補助（ほじょ）線をひいて考えていきましょう。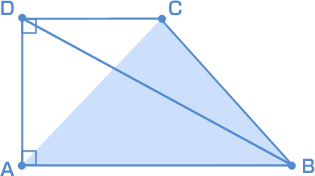 底辺が共通で高さが同じなので、三角形ABDの面積と、三角形ABCの面積は同じになりますね。 同様に、三角形ACDと三角形BCDの面積は同じです。 だから台形ABCDの面積は、三角形ABDと三角形ACDの面積の和となります。 小問（1）の「考え方と答え」で示したグラフより、 三角形ABDの面積は点PがBに着いたとき、三角形ACDの面積は点PがCに着いたときですから、 三角形ABDの面積 ＋ 三角形ACDの面積 ＝ 432 ＋ 216 ＝ 648  |
| ＜問題2 （3）の考え方と答え＞ |
| 台形ABCDの面積の半分ということは、 648 ÷ 2 ＝ 324（cm²） のときですね。 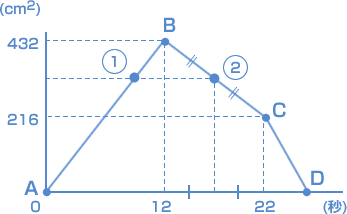   点Pが辺AB上を動いていますから、 ADを長さ24cmの底辺とし、APの長さ（高さ）を□cmとして、このときの面積が324cm² だから、 24 × □ ÷ 2 ＝ 324 □ ＝ 27（cm） 27cmの道のりを毎秒3cmで移動するのにかかる時間は、 27 ÷ 3 ＝ 9 → 9秒後  上のグラフより、324cm² は 432cm² と 216cm² のちょうど中間点であるとわかります。  （12 ＋ 22）÷ 2 ＝ 17 → 17秒後  |
