算数｢点の移動・図形の移動｣［中学受験］
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題4 |
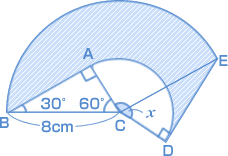 右の図のように、角の大きさが30°、60°、90°の三角形ABCが頂点Cを中心にして回転し三角形DECの位置にきたとき、辺ABと辺CEは平行になりました。（1）角χ の大きさは何度ですか。 （2）辺BCの長さが8cmのとき、しゃ線部分の面積は何cm² ですか （函館ラ・サール中 2007年） |
| ＜問題4 （1）の考え方と答え＞ |
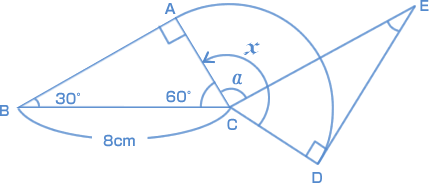 辺ABと辺CEが平行になることから、角ａは90°であるとわかります。よって、角χ は、 90° ＋ 60° ＝ 150°  |
| ＜問題4 （2）の考え方と答え＞ |
| まず辺ACの長さを求めておきます。
では、しゃ線の部分の面積を求めていきます。 「半径8cm、中心角150°のおうぎ形の面積 ＋ 三角形DECの面積の和」 ここから、 「半径4cm、中心角150°のおうぎ形の面積と、三角形ABCの面積」をひくと、しゃ線の部分の面積です。  三角形ABCと三角形DECは同じ面積ですから、  ＝ 62.8  ここでも、「× 3.14」は最後にかけました。 この単元では工夫する計算がよく出てくるので、しっかり練習してくださいね。 |
関連するおすすめの記事
みんなが読んでる！おすすめ記事
- 算数｢面積と角度｣［中学受験］
- 【自由研究テーマ 中学生】地球温暖化をデータから探る
- 学力や入試の本質を知ることが大事[2012年度入試で何が問われたか＜算数＞ お子さま主導型で成長を実感できる算数 第2回]
- 算数｢点の移動・図形の移動｣［中学受験］
- 【自由研究テーマ 中学生】新聞紙が野菜のせん度を守る効果を調べる
- 向き合い方ひとつでお子さまは変わります[2012年度入試で何が問われたか＜算数＞ お子さま主導型で成長を実感できる算数 第4回]
- 算数｢面積と角度｣［中学受験］
- 【自由研究】日本人ノーベル賞受賞者の研究を調べる ＜中学生＞
- お子さまの気持ちに寄り添って[2012年度入試で何が問われたか＜算数＞ お子さま主導型で成長を実感できる算数 第5回]
