算数｢点の移動・図形の移動｣［中学受験］
| 問題5 |
   （3）重なった部分の面積が8cm² になるのは何秒後と何秒後ですか。 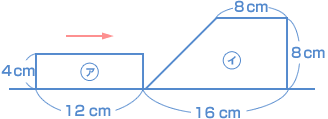 （報徳学園中 2007年 2次A） |
| ＜問題5の考え方と答え＞ |
| この問題は2つの図形の重なり具合をしっかりと図に表すことが重要です。 |
| ＜（1）の考え方と答え＞ |
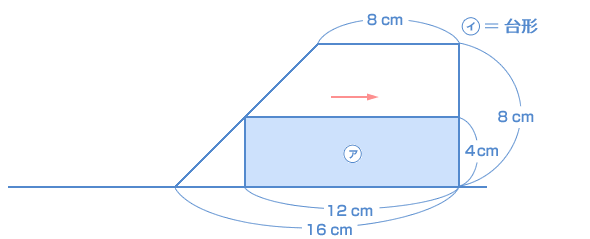
  台形の面積を求めるには、上底と下底と高さがわかっていなくてはいけません。そこで、ここでわかっていない上底の長さを求めます。 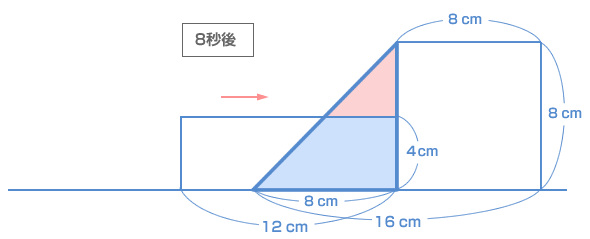 ピンク色の三角形は、太線の三角形と相似ですね。相似比は1：2ですから、 重なった台形の上底の長さは、  よって、求める台形の面積は、 （4 ＋ 8）× 4 ÷ 2 ＝ 24  |
| ＜（2）の考え方と答え＞ |
   16cmを秒速1cmで右へ移動したので、 16 ÷ 1 ＝ 16  |
| ＜（3）の考え方と答え＞ |
まず、重なった部分の面積が8cm² になるときの図をかいてみます。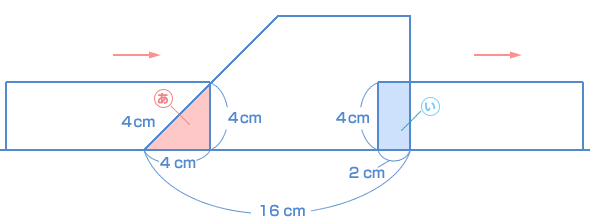   4 ÷ 1 ＝ 4（秒後）  （16 ＋ 12 − 2）÷ 1 ＝ 26（秒後）  |
さて、いかがでしたでしょうか。
「点の移動・図形の移動」の単元にまず慣れてもらうために、難問（なんもん）よりも基本的な問題を取り上げました。
初めに言いましたように、類似した問題を数多くこなして、基本をまず定着させてください。
そのためにも、図形が移動していく様子を自分でかく練習が重要ですよ。塾（じゅく）の授業で、生徒たちは先生のかいた図をノートに写すんですが、写すのが精一杯（せいいっぱい）で、イメージをなかなかつかめず家に帰る生徒がほとんどでした。この機会に、じっくり自分でノートに移動の図をかいてください。
文章題にもまして、この図形の問題が解けたときの感動は、きっとますます算数好きにしてくれるでしょう。
合格総理大臣 ミスター・ツカム
