算数｢面積と角度｣［中学受験］

問題3

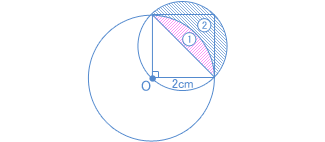（久留米大学附設中　2007年）

＜問題3の考え方と答え＞

　　　　＝ 3.14 − 2
　　　　＝ 1.14（cm²）

でも、円の直径が正方形の対角線になっています。

このパターンはよく出てきますから、覚えておいてください。
小さいほうの円に注目して、図をかきます。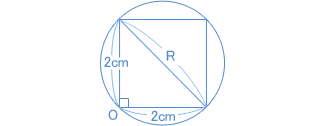

ここで確認しておきましょう。
正方形の面積の求め方は次の2通りがありますね。

　　　　正方形の面積＝　1辺 × 1辺

　　　　正方形の面積＝　対角線 × 対角線 ÷ 2

正方形の面積は　2 × 2 ＝ 4（cm² ）です。

対角線の長さを R とすると、正方形の面積は、

　　　　R × R ÷ 2 ＝ 4　　となり、
　　　　R × R ＝ 8 　　となりました。

次に、小さいほうの円の半分の面積を、Rを使って式に表してみます。

　　　　

整理すると、

　　　　

　　　　R × R ＝ 8　　　　だから、

半円の面積は、

　　　　

　　　　3.14 − 1.14 ＝ 2（cm² ）

ミスター・ツカム

大人気メールマガジン「コロンブス的・超発想で中学受験を成功させる方法」の発行人で、中学受験カウンセラー。メルマガは殿堂入りを果たす。理科・替え歌暗記法のCD『愛のメモリーTM』も作成。

子育て・教育Q&A