算数｢平面図形と比（2）｣［中学受験］
| 問題5 |
図の平行四辺形は辺BCが12cmで、辺BCを底辺としたとき高さは10cmです。点E、F、G、Hは辺ABを5等分した点です。点L、M、Nは辺CDを4等分した点です。さらに点P、QはENを3等分した点です。このとき、斜線部分の面積は cm²です。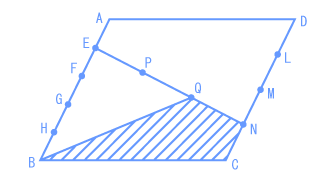 （青山学院中 2008年） |
| ＜問題5の考え方と答え＞ |
| 求める四角形の面積を2つに分けて考えましょう。 次の図のように補助線をひきます。 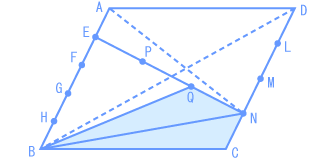 平行四辺形ABCDの面積は、 12 × 10 ＝ 120（cm²） ですね。 求める四角形QBCNの面積は、次の考え方で求められます。 四角形QBCNの面積 ＝ 三角形BNQの面積 ＋ 三角形BCNの面積 では、それぞれの三角形の面積を求めていきましょう。 【三角形BNQ】   【三角形BCN】  よって、求める四角形QBCNの面積は、 16 ＋ 15 ＝ 31 （cm²）  |
いかがでしたか？
図形問題には算数のおもしろさがいっぱいあふれていますよね？ そう思いませんか？
相似の図形を見つけたときの喜び、こう考えたらイケるんじゃない？ …とヒラメいて解けたときの快感。
キミもどんどん解けるようになってきたら、この楽しさを体感できるよ。
「絶好調！」と声に出してがんばってください。
合格総理大臣 ミスター・ツカム
