算数｢面積と角度｣［中学受験］
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題4 |
図のように、点Cを中心として直角三角形ABCを矢印の向きに回転させました。円周率を3.14とするとき、次の問いに答えなさい。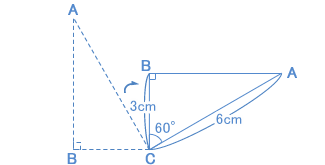 （1）90°回転させたとき、辺ABが動いてできる部分の面積は何cm² ですか。 （2）回転させた後、辺ABが動いてできる部分の面積と、辺BCが動いてできる部分の面積の差が37.68cm² でした。何度回転させましたか。 （世田谷学園中 2007年） |
| ＜問題4 （1）の考え方と答え＞ |
| 辺ABが動いた様子を図にかいてみましょう。 点Aと点Bの動いた様子をかけばいいんですよ。難（むずか）しく考えないでね。 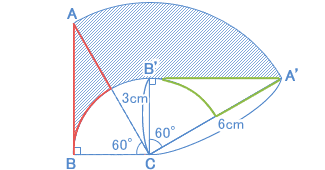 これも回転移動のパターンですから、次のことをよく確かめて、覚えておきましょう。 まず、求めるのは青い斜線（しゃせん）の部分の面積ですね。 そして、図で、緑の線で囲まれた部分の面積と、赤い線で囲まれた部分の面積は等しいです。 なぜかわかりますか？ どちらも、三角形ABCの面積から、同じ面積のおうぎ形（中心角60°）をひいたものだからです。 だから、辺ABが動いてできた部分の面積は、 大きいおうぎ形の面積 − 小さいおうぎ形の面積 で求められます。   計算の工夫をわすれずにね！    ＝ 6.75 × 3.14 ＝ 21.195（cm²）  |
| ＜問題4 （2）の考え方と答え＞ |
ここで、□°回転させたとして図をかきます。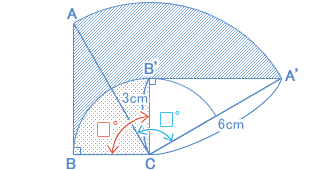 小問（1）と同じように考えると、 辺ABが動いてできる部分の面積は おうぎ形ACA" − おうぎ形BCB" で求められますね。 ここで求めようとしているものは、  整理すると、 （おうぎ形ACA" − おうぎ形BCB" ）−（おうぎ形BCB" ） となり、 おうぎ形ACA" − おうぎ形BCB" × 2 です。 これが、37.68 cm² になるのですから、 動いた角度を□°として、     これが、37.68 cm² なので、      |
関連するおすすめの記事
みんなが読んでる！おすすめ記事
- 中学入試問題学校別分析【武蔵中・算数】攻略法は満点をとること
- わかりやすい学校案内（パンフレット）とは？ [中学受験]
- ノートや日記の字が雑で困る［教えて！親野先生］
- 2012年度入試問題 学校別分析1 【雙葉中、女子学院中】[2012年度入試で何が問われたか＜算数＞ 首都圏上位10校の問題を徹底分析 第2回]
- 「学校に行きたくない」と子どもが言ったらどうする？ ほとんどの場合、保護者は自分の子どものことをわかっていない
- 社会の資料の読み取りが苦手な小学生・・・問題演習だけでは克服できないので注意！
- 2012年度入試問題 学校別分析3 【武蔵中、駒場東邦中、栄光学園中】[2012年度入試で何が問われたか＜算数＞ 首都圏上位10校の問題を徹底分析 第4回]
- 新指導要領の先取り、本当に大丈夫？ 初体験に戸惑う学校
- 子どもと信頼関係を築くための会話術を伝授します！【小学校低学年向け】
