算数｢面積と角度｣［中学受験］
今回もツカム先生が、全国の中学入試問題から厳選（げんせん）した問題を解説していきます。いっしょに取り組んで、得意単元を増やしていきましょう。
■算数「面積と角度」
こんにちは、合格総理大臣 ミスター・ツカムです。
今回は「面積と角度」を取り上げます。ここでのポイントは、あたえられた問題の中に自分で補助線（ほじょせん）をひいたり、図形を移動させたりするコツをつかむことです。
それには、多くの問題にふれて経験を積んでおくことが大事ですね。キミの志望校の出題傾向（けいこう）も、しっかりおさえておいてくださいね。
では、問題を見ていきましょう。
| 問題1 |
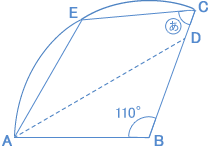 右の図は、点Bを中心とする円の一部です。いま、ADを折り目として折ったとき、点Bが円周上の点Eに重なりました。 （浦和明の星女子中 2008年） |
| ＜問題1の考え方と答え＞ |
| 円の一部であること、折り返したこと、この2つのことからわかることを、 図にかき加えてみます。 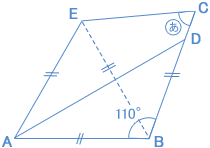 AB ＝ EB ＝ CB 半径ですから等しいですね。 AB ＝ AE ADを折り目として折ったから等しいですね。 そうすると三角形EABは、 AB ＝ EB ＝ AE で、正三角形になります。 だから、 角EBA ＝ 60°で、 角EBC ＝ 110°− 60°＝ 50° 三角形BCEは、CB ＝ EB で二等辺三角形 です。  （180°− 50°） ÷ 2 ＝ 65°  |
| 問題2 |
下の図で、CはAB上の点、EはCD上の点、AC＝CD、AE＝BDです。このとき、角アは 度です。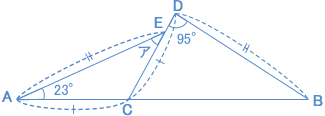 （洛南高校附属中 2007年） |
| ＜問題2の考え方と答え＞ |
| 続いても角度の問題です。 これまでは、補助線（ほじょせん）をひいて考える、というパターンが多かったですね。 この問題は、ちょっと図形を移動させてみるのがポイントです。 等しい辺の組み合わせが2つもあり、なんとかこれを使いたいですが、この図のままでは、どうしようもありません。 そこで、AC ＝ CD なので、この2つの辺が合わさるように、三角形ACEを切りはなしてひっくり返します。 下の図のようになりました。 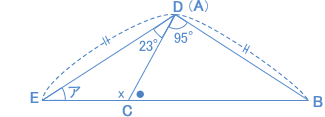 なんだか、二等辺三角形ができたようでうれしくなりますね。 でも、ひとつ確認（かくにん）が必要です。ECBは一直線なのでしょうか？ 一直線なら、DE ＝ DB より、二等辺三角形となります。 上の図の、● と × の角度に注目すると、ひっくり返しても角度は同じままですね。 ですから、ECBは一直線であり、三角形DEB（AEB）は、二等辺三角形です。 よって、アの角度は、 （180°− 95°− 23°） ÷ 2 ＝ 31°  |
