算数｢面積と角度｣［中学受験］
| 問題5 |
図のように長方形の中に、各辺に接して半径5cmの2つの円が重なって入っています。アの部分の面積がイの部分の面積の2倍と等しいとき、図のABの長さは何cmになるか答えなさい。 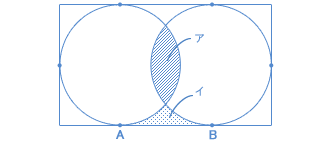 （西大和学園中・県外 2008年） |
| ＜問題5の考え方と答え＞ |
| このような問題は、経験がモノをいいますね。 同じような問題にふれていると「ピッ」とひらめきます。 いや、センスの良い人は初めてでもひらめくかもしれません。 基本的な問題で以下のようなものがありました。 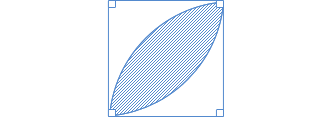 斜線（しゃせん）の部分の面積を求めなさい…という問題です。  その応用的な問題です。 補助線をひき、点D、Cと、図形で区切られたそれぞれの場所をウ、エ、オとして、図にかきこみます。 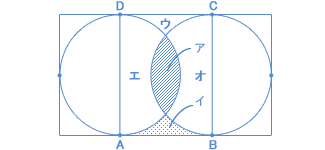 ABの長さを求めるんですね。 長方形ABCDの面積がもしわかるなら、たては10cmだから解決です。 この長方形の面積を、半円2つの面積で計算できないかなあ？ …という発想です。 問題文から、 ア ＝ イ ＋ ウ です。 そうすると、 左の半円の面積 ＋ 右の半円の面積 ＝ エ ＋ ア ＋ ア ＋ オ …と、なりました。 ここで、 ア ＝ イ ＋ ウ を入れてみます。 左の半円の面積 ＋ 右の半円の面積 ＝ エ ＋ ア ＋ イ ＋ ウ ＋ オ ＝ 長方形ABCDの面積 ですね。 つまり、  よって、ABの長さは、 5 × 5 × 3.14 ÷ 10 ＝ 7.85（cm）  |
いかがでしたか？
ほかの問題にもチャレンジして、少しずつ「ヒラメキ脳（のう）」をつくっていってくださいね。
合格総理大臣 ミスター・ツカム
