算数｢平面図形と比（2）｣［中学受験］
| 問題4 |
下図において、四角形DEFG、四角形GHCIはともに正方形で、角AJD=90°、GH＝2cm、FH=5cmとします。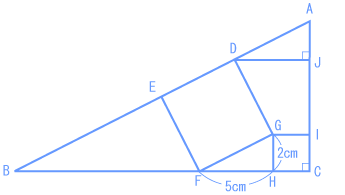 （1）AJの長さは cmです。 （2）三角形ABCの面積は cm² です。 （芝中 2007年） |
| ＜問題4 （1）の考え方と答え＞ |
正方形DEFGの周りに補助線（ほじょせん）をひきます。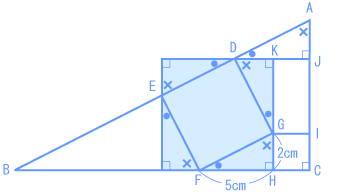 正方形の中に正方形がある…という図になりました。 これはよく使う考え方なので、覚えておいてくださいね。 三角形GFHと合同な三角形が、ほかに3つできました。 DK ＝ 2cm、四角形GHCIは1辺が2cmの正方形だから、 DJ ＝ DK ＋ KJ ＝ 2 ＋ 2 ＝ 4（cm） です。 上の図に示したとおり、対応する頂点（ちょうてん）の角度が等しいので、 三角形ADJ と 三角形GFH は相似であるとわかりますね。相似比は4：5です。 だから、   |
| ＜問題4 （2）の考え方と答え＞ |
小問（1）でAJの長さがわかったので、図にわかっている長さをかきます。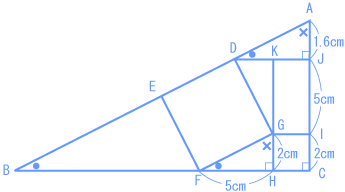 そうすると、あとはBCの長さがわかれば、三角形ABCの面積が求められます。 三角形GFHと三角形ABCは相似で、GH：AC＝FH：BCです。 これに数値（すうち）を当てはめていくと、次のようになります。 2 ： （1.6 ＋ 5 ＋ 2） ＝ 5 ： BC よって、  ＝ 21.5（cm） 三角形ABCの面積は、 21.5 × 8.6 ÷ 2 ＝ 92.45（cm²）  |
