算数「平面図形と比(2)」[中学受験]
お気に入りに登録
今回もツカム先生が、実際の入試問題の解き方・考え方をていねいに解説していきますから、いっしょに取り組んで得意単元にしていきましょう。
■算数「平面図形と比(2)」
こんにちは。合格総理大臣 ミスター・ツカムです。
今回は「平面図形と比」についていっしょに考えていきましょう。
この単元も、難関校(なんかんこう)はほぼ必ずといっていいほど出題しています。ポイントは、自分で補助線(ほじょせん)などをかきこんで考えていけるか、相似の三角形が見つかるか、などです。
何度もよく似た問題を解いていけば、自然とできるようになりますから、がんばってくださいね。
ではさっそく、過去問を見ていきましょう。
| 問題1 |
| 面積が9cm²である正方形ABCDがあります。下の図のように、この正方形の各辺を3等分した点をつないで正方形EFGHを作りました。さらに、正方形EFGHの各辺を3等分した点をつないで、正方形OPQRを作りました。 このとき、正方形EFGHと正方形OPQRの面積を求めなさい。 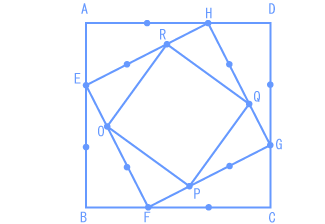 (浦和明の星女子中 2008年) |
| <問題1の考え方と答え> |
| まずは三角形AEHの面積を求め、そこから正方形EFGHの面積を求めていきましょう。 問題文から、正方形ABCDの面積は9cm²とわかっていますから、 9 = 3 × 3 より、正方形ABCDの1辺の長さは3cmです。 これを3等分しているので、辺AEの長さは1cm、辺AHの長さは2cmとなり、 三角形AEHの面積は、 1 × 2 ÷ 2 = 1(cm²) よって、正方形EFGHの面積は、  ここまでで、 正方形ABCDと正方形EFGHの面積比は、9:5 とわかりましたね。 正方形EFGHと正方形OPQRの面積比も、同じく 9:5 です。  |
| 問題2 |
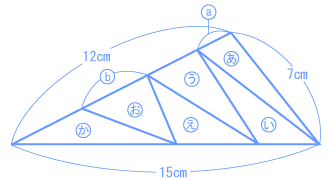 (岡山中 2008年) |
| <問題2の考え方と答え> |
6つの三角形の面積は等しいので、 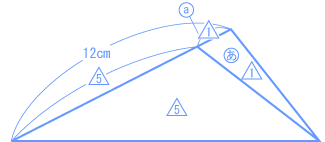 面積比=底辺比 だから、 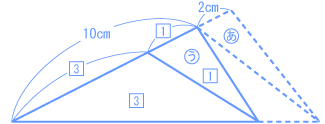 上の図のように整理して、面積比=底辺比 なので、 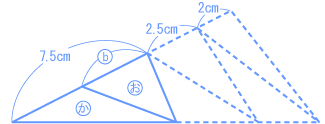  7.5 ÷ 2 = 3.75(cm) |













![算数「平面図形と比(2)」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu19/01.gif)
![算数「平面図形と比(1)」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu_line.gif)








