算数「平面図形の面積と角度」［中学受験］
| 問題6 |
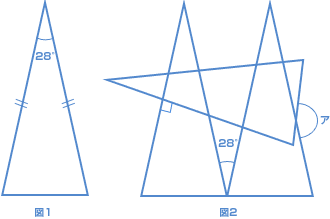 右の図1の二等辺三角形を、図2のように3つおいたとき、アの角度は何度ですか。（早稲田中 2008年） |
| ＜問題6の考え方と答え＞ |
| まずは、次のように、図にA～Gまで点をつけました。 同じ二等辺三角形をならべているので、 底角はすべて （180°− 28°）÷ 2＝ 76° 角Bも76°だとわかります。 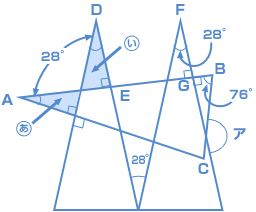  頂点Aの角と頂点Dの角が等しく、対頂角が等しいからです。 …ということは、角AED ＝ 90°ですね。 そして、錯角（さっかく）が28°で同じなので、DEとFGは平行です。 平行での同位角は等しいから、角AGFも90° よって、アの角の大きさは、三角形BCGの外角により、 90°＋ 76°＝ 166°  |
| 問題7 |
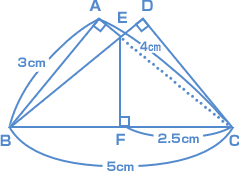
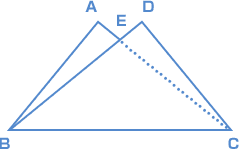 右の図はたて3cm、横4cm、対角線の長さが5cmの長方形を、対角線を折り目として折って作った五角形である。このとき、AEの長さは （1） cm、 五角形ABCDEの面積は （2） cm²である。 にあてはまる数を求めなさい。 （灘中 2008年） |
| ＜問題7の考え方と答え＞ | ||
| 最後に難関中の平面図形の問題です。 さっそく、（1）のAEの長さをさぐっていきましょう。 これは自分で補助線（ほじょせん）をひかなくては解けません。 でもポイントは「相似形」を利用することですよ。 「苦しいときの神だのみ」…じゃなく、「苦しいときは相似見つけ！」…なのです。
また、三角形ABCと三角形CEFは相似だから、 4 ： 5 ＝ 2.5 ： C   続いて、（2）について考えてみましょう。 五角形ABCDE が、三角形ABE と 三角形BCD の、2つの三角形に分割（ぶんかつ）できることに気がつきましたか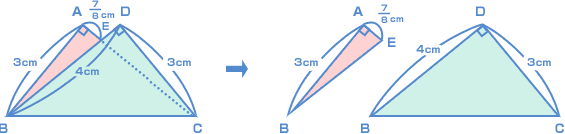？  このことが発見できれば、あとは簡単（かんたん）ですね。（1）でわかったAEの長さを利用して、2つの三角形の面積を求めればいいのです。 こんなふうに、小問がいくつかある問題では、先の小問の答えが、あとの小問を解くカギになることが多いですよ。 五角形ABCDEの面積 ＝ 三角形ABEの面積 ＋ 三角形BCDの面積   |
いかかでしたか？
復習すると、「平面図形の面積と角度」の問題は、
「内角・外角の和」
「三角形、四角形の特ちょう」
「平行線の特ちょう」
「相似とその比」
…これらを組み合わせて考えると、必ず答えにたどり着きます。
角度と面積の問題、ミスター・ツカムは小学生のころ大好きでした。すぐに答えを見ないで、ウンウン考えて「パッ」とひらめいたときの快感はいまだに覚えていますよ。人間は「わかる喜び」をだれでももっています。キミもますます算数大好きになって、いっぱい感動してくださいね。
合格総理大臣 ミスター・ツカム
