算数「平面図形の面積と角度」［中学受験］
| 問題2 |
 図のように、正方形の中に半径の等しい円とおうぎ形が入っています。正方形の面積が200cm²であるとき、円周率を3.14とすると斜（しゃ）線の部分の面積は cm²です。（甲陽学院中 2008年） |
| ＜問題2の考え方と答え＞ |
| 次もアタマの体操（たいそう）のような問題ですね。問題を見た瞬間（しゅんかん）にひらめいた人も多いはずですね。 まず、この正方形に対角線をひきます。 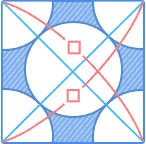 対角線の長さを□として、□を使ってこの正方形の面積は表せないでしょうか？ 正方形はひし形の一種ですから、 面積は （対角線）×（対角線）÷ 2 で求められますよね。 □ × □ ÷ 2 ＝ 200 …という式が成り立ちます。 □ × □ ＝ 400 ですから、 □ ＝ 20 となりました。 これは、中に入っている円とおうぎ形の半径の4倍の長さです。 20 ÷ 4 ＝ 5 （cm） …円の半径の長さ 正方形に入っているのは、半径5cmの円が2つ分ですから、その面積は、 5 × 5 × 3.14 × 2 ＝ 157 （cm²） だから、斜線の部分の面積は、 200 − 157 ＝ 43  |
| 問題3 |
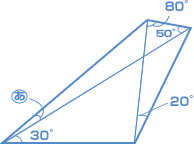  （フェリス女学院中 2007年） |
| ＜問題3の考え方と答え＞ | ||
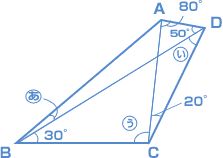
今度は角度を求める問題です。さまざまな問題がありますが、二等辺三角形、正三角形、平行四辺形、内角、外角などの特ちょうを使って考えていけば必ず解けますので、がんばってみてください。
三角形ACDの内角の和より、  このことから、三角形ACD も 三角形BCD も二等辺三角形であるとわかります。 だから、CD＝CA、CD=CB で、CA＝CB となり、 三角形ABCも二等辺三角形です。 三角形BCDの内角の和より、  二等辺三角形ABCの底角は？ （180°− 100°）÷ 2 ＝ 40°  40°− 30°＝ 10°  |
