算数「平面図形の面積と角度」［中学受験］

こんにちは。ミスター・ツカムです。
前回に引き続き、今回も平面図形を取り上げます。「平面図形と比」と同じぐらい出題頻度（ひんど）の高い「面積と角度」の入試問題にチャレンジしていきましょう。

ここの問題は「パズルっぽい」というか、算数が大好きな人は得意な単元ですよね。あまり得意でない人はぜひ今回、克服（こくふく）してください。
自分で点の名前（点Aとか）を決めたり、補助線（ほじょせん）をひいたりして考えることに慣れてしまえば、案外すぐ得意になるかもしれませんよ。

わからなくても、すぐに解説を見ないで、「○分間は考えよう」…と考える時間を決めてアタマを使ってみてください。そうしたうえで解説を読むと「な～るほど。こう考えるのか！」と感動が大きいです。算数は「感動する教科」ですからね。

では、ミスター・ツカムといっしょにがんばっていきましょうね。

問題1

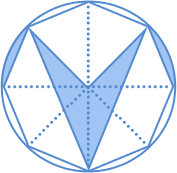図のように、半径10 cmの円の中に正八角形があります。影（かげ）をつけた部分の面積は 　　　 cm²です。ただし、円周率は3.14とします。 （神戸海星女子学院中　2008年）

＜問題1の考え方と答え＞

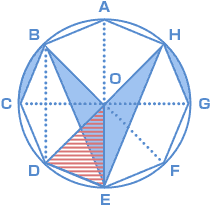
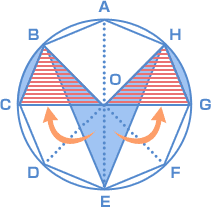
まずは、パズル的な問題でアタマのウォーミングアップをしましょう。 正八角形の頂点を、A、B、C、D、E、F、G、H、 円の中心を O とします。 初めに、三角形OBE について考えてみます。 正八角形の性質上、BD と AE は平行になっています。 だから、三角形OBE の底辺をOEとすると、 高さが同じなので、三角形ODE と 三角形OBE の面積は等しいことに気づきます。