算数｢立体｣［中学受験］
ツカム先生からの例題も、立体の問題の中でも取り組みやすい基本的な良問がそろっています。今回もツカム先生としっかり勉強して、得意単元を増やしましょう。
■算数「立体」
こんにちは、合格総理大臣 ミスター・ツカムです。
今回は「立体」を取り上げます。この単元は「空間的な想像力」が必要になってきます。だから苦手とする人が多いと思います。
問題も、本当に多くのパターンが登場してきます。キミの志望校の出題傾向をよく研究して、しぼった練習をしたほうがよいでしょう。
ですから今回は、わりと基本的な問題を取り上げました。ぜひ、マスターしてくださいね。
| 問題1 |
断面が図1のような、直方体の中をくり抜（ぬ）いた形のコンクリートブロックがあります。断面は直径5cmの半円と直線とでできています。このブロックを、たて47cm、横76cmで、35cmの深さまで水が入っている直方体の水そうに図2のように完全に沈（しず）めたところ、水面が2.5cm上昇（じょうしょう）しました。ブロックの横とたての長さはそれぞれ40cm、20cmです。このブロックの高さを求めなさい。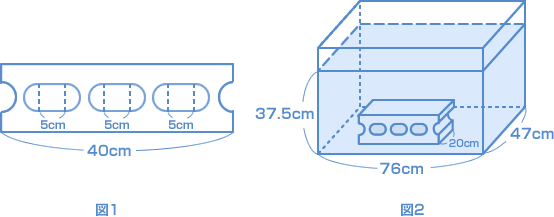 （六甲中 2008年） |
| ＜問題1の考え方と答え＞ | |||||||||||||||||||||
| これは基本的な問題ですね。キミもスグ解き方は思いついたでしょ？ 水面が2.5cm上昇したので、コンクリートブロックの体積がわかりますね。 水面が上昇した分の水の量と、コンクリートブロックの体積は等しいので、 47 × 76 × 2.5 ＝ 8930（cm³） 次にこのブロックの高さを□cmとして、体積を求める式を立てます。 （図1の面積）× 20 → ブロックの体積 になります。 問題文の図1の面積を、□を使って表します。 たて□cm、横40cmの長方形から、 直径5cmの円4個、1辺5cmの正方形3個をくり抜いた面積です。 こうかけますね。 □ × 40 −（2.5 × 2.5 × 3.14 × 4 ＋ 5 × 5 × 3） ＝ □ × 40 − 153.5 …となりました。 このブロックの体積は、8930 cm³ だから
 |
| 問題2 |
容器に水を入れてもれないようにふたをします。これを図1のようにして、水平な床（ゆか）に置くと、水の深さは5cmになりました。これを図2のようにして、水平な床に置くと、水の深さは cmになります。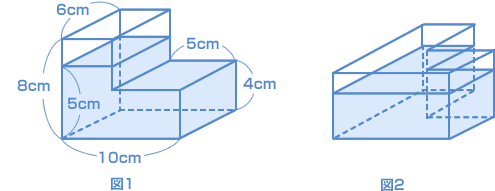 （甲南女子中 2007年） |
| ＜問題2の考え方と答え＞ |
| このパターンもよく見られますから、基本をきっちりおさえておきましょうね。 2つの考え方をします。 まずは、ひとつ目の考え方。地道に計算してみますね。 図1の水の量を2つの直方体に分けて計算すると？  図2のように横にたおすと、容器の底の表面積が変わります。 体積は、 表面積 × 高さ で求められますから、 底の表面積は、 8 × 10 − （ 8 − 4 ）× 5 ＝ 60（cm²） 水の深さを□cmとすると？ 60 × □ ＝ 270 □ ＝ 270 ÷ 60 □ ＝ 4.5  次に、別の考え方。 面積図を使って考えてみましょう。 図1の状態を真横から見ると、 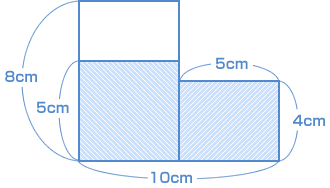 このような面積図で表せますね。 斜線（しゃせん）の部分は水が入っている状態です。 斜線の部分の面積は 5 ×（ 10 − 5 ）＋ 4 × 5 ＝ 45（cm²） です。 全体の面積 8 × 10 − （ 8 − 4 ）× 5 ＝ 60（cm²） に対して、斜線の部分の面積は、   図2 のように置くと、容器の高さは 6cm なので、  |
