｢電流｣理科｢電流｣［中学受験］
| 問題4 |
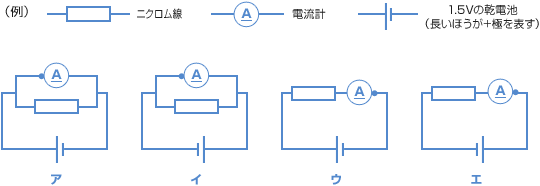
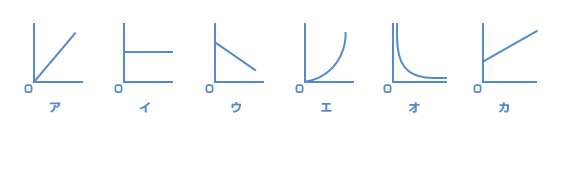
断面積や長さの異なる9種類のニクロム線を準備して、以下の実験を行いました。各問に答えなさい。 【実験1】断面積や長さの異なるニクロム線に1.5Vの乾電池（かんでんち）をつないで、電流を流したところ、右の結果が得られた。 問1 【実験1】で電流計を用いて電流を測った。電流計をどのように接続したか、次のア～エから正しいものを1つ選び、記号で答えなさい。ただし、●は電流計の赤い端子（たんし）を表している。 【実験1】と同じニクロム線を使って、いろいろな回路を作り、実験を行った。ただし、ニクロム線の断面積や長さは、（例）のように表す。 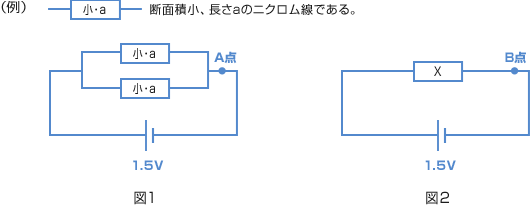 問3 断面積小、長さaのニクロム線を2本並列につなぎ、図1のように1.5Vの乾電池につないだ。図1のA点を流れる電流と等しい電流を、ニクロム線Xを1本だけ使って、図2の回路のB点に流したい。ニクロム線Xとして正しいものを次のア～カから1つ選び、記号で答えなさい。 （早稲田中 2005年・第2回） |
| ＜問題4 問1の考え方と答え＞ |
| 電流計のつなぎ方を問われていますよね？ ポイントは、 ・回路に直列につなぐ ・電流計の＋の端子（赤い端子）を、乾電池の＋極につなぐ この2点です。  |
| ＜問題4 問2の<1>の考え方と答え＞ |
  |
| ＜問題4 問2の<2>の考え方と答え＞ |
長さa（8cm）のニクロム線で見てみましょう。 断面積が6.3 mm² から12.6 mm² （2倍）になると、流れる電流の大きさは、0.03Aから0.06A（2倍）になり、断面積が18.9 mm² （3倍）になると、電流は0.09A（3倍）になっています。これは比例の関係ですね。 |
| ＜問題4 問3の考え方と答え＞ |
| 長さが同じニクロム線を並列につなぐと、2つのニクロム線の断面積を合わせた、太いニクロム線1本とみなすことができます。 これは知識として覚えておいてください。 イメージしにくい人のために、「かまぼこ」でお話ししますね。 長さが同じ「かまぼこ」の底面の部分を合わせると、太い「かまぼこ」になりますよね？（笑） そんな感じです。  だから（小・a） 2つを並列に並べると、6.3 mm² の2つ分、つまり12.6 mm² の断面積の（中・a）と置きかえることができます。  |
| ＜問題4 問4の考え方と答え＞ |
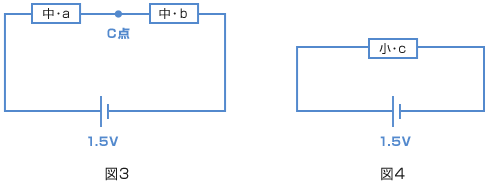
| 断面積が同じニクロム線を直列につなぐと、どうなると思いますか？ さっきの発想で考えてみましょう。 そうです！ 2つの長さを合計した1本のニクロム線と同じになります。 だから、（中・a）＋（中・b）は？ 8 ＋ 16 ＝ 24（cm）の（中・c） と同じ になりますね。 表から、図3のC点に流れる電流の大きさは、0.02A だとわかります。 では、図4の回路全体に流れる電流は？ ニクロム線が（小・c）だから、表から、0.01A だとわかります。 ですから、図3のC点には、図4の2倍の電流が流れています。  |
| ＜問題4 問5の考え方と答え＞ |
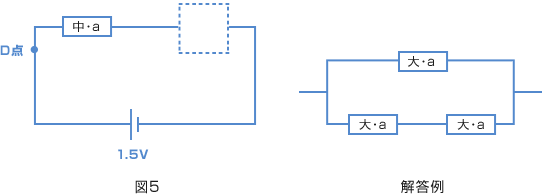
| これは問4がヒントになっていますよ。理科も算数と同じように、大問の中にいくつかの小問があるときは、先の小問がヒントになっていることがあります。 考えに行きづまったら思い出してね。 図3の回路で0.02A の電流が流れているので、点線のボックスの中がニクロム線（中・b）1本と置きかえられる組み合わせをさがせばいいね。 ちなみに解答例のつなぎ方だと、どのニクロム線1本と置きかわるか？考えてみましょう。  上の例とは逆の考え方ですね。  まとめると、こうなりました。 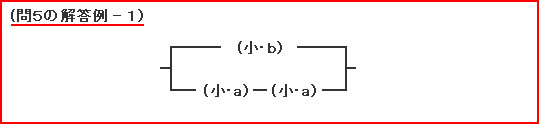 このほかにも、いくつかのつなぎ方が考えられますね。  まとめると、次のようになります。 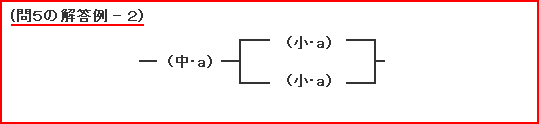 ほかにもあるので、考えられる人は挑戦（ちょうせん）してみましょう。 |
以上で、今回の「電流」はおしまいです。どうでしたか？
1問1問ゆっくり考えたら楽しくて、得意単元になりそうな気がするでしょ？ この際、「ぼくは（わたしは）電流が得意なんだ！」…と、宣言（せんげん）しちゃいましょう。何度かくり返し解いてみて定着させようね。
合格総理大臣 ミスター・ツカム
