｢立体｣算数｢立体｣［中学受験］
| 問題5 | ||||
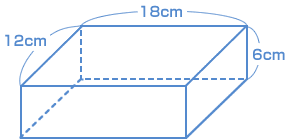 図のような直方体があります。この直方体を分割（ぶんかつ）して、6個の同じ形の直方体または立方体を作ろうと思います。すべての分割のしかたを考えるとき、次の問いに答えなさい。
（同志社国際中 2007年） |
| ＜問題5 （1）の考え方と答え＞ | |||||||||||||||
| どんなふうに分割したら6個の同じ形ができるか、 ためしに、思いついた切り方を図にかきこんでみましょう。 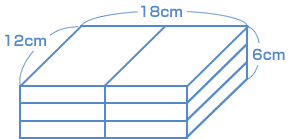 縦（たて）12cmはそのまま、横18 cm を2等分、高さ6cmを3等分に切り分け、 6つの直方体を作りました。 上の図の切り方を（1，2，3）と表します。 この表し方で、6等分する切り方をすべてあげていきますよ。 （1，2，3） （1，3，2） （2，1，3） （2，3，1） （3，1，2） （3，2，1） （1，1，6） （1，6，1） （6，1，1） このように、9通りの分割方法がありますね。 「やっほー、答えが出た！」って早合点（はやがてん）しないでね。同じ形の直方体があるかもしれません。 調べるために、この表し方を「辺の長さ」で書き直します。 （1，2，3）を辺の長さで書き直すと、 → ［12，9，2］ となります。 見やすいように、短い順に書きます。 → ［2，9，12］ そうすると、上の9通りの直方体は以下のように書き直せます。
★ と ☆ は同じ形の直方体になりますから、それぞれ1回だけ数えると、 答えは7種類です。  | |||||||||||||||
| ＜問題5 （2）の考え方と答え＞ | |||||||||||||||
| 上のうち、3つの辺の長さの和が最も小さいのは、18cmの、 ［6，6，6］ ですね。  |
初めにも書きましたように、「立体」にはさまざまなパターンの問題があります。テキストや参考書の問題をすべて理解しようとしないで、まずは基本的な問題を定着させましょう。
あとは、志望校の傾向に合った演習をくり返してくださいね。それがこの「立体」という単元の、カシコい取り組み方ですよ。空間的な考え方ができるようになったら、よりいっそう算数が好きになることまちがいなしです。
合格総理大臣 ミスター・ツカム
