算数｢速さ（流水算・時計算）｣［中学受験］
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題3 | ||
（1）静水での船の速さは時速何kmですか。 （2）川の流れの速さは時速何kmですか。 （3）船がA地、B地間を往復するのにかかる時間は、休みをふくめて何時間何分ですか。 （神奈川大学附属中 2008年） |
| ＜問題3 （1）の考え方と答え＞ |
| まず、それぞれのグラフの直線部分は、どんな状態なのか？ を、しっかりと理解しておきましょう。 図にかきこんでみます。 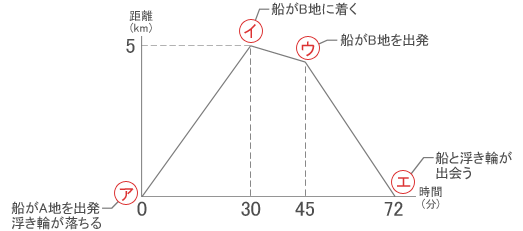  つまり、 （下りの速さ）−（浮き輪の速さ ＝ 川の流れの速さ） で、距離が増えていきます。 基本公式は 下りの速さ ＝ 船の静水時の速さ ＋ 川の流れの速さ なので、 これは、この船の静水時の速さを表していますよね。 グラフから、5 kmを30分で進んでいるので、 5 ÷ 0.5 ＝ 10  |
| ＜問題3 （2）の考え方と答え＞ |
 基本公式 上りの速さ ＝ 船の静水時の速さ − 川の流れの速さ より、    船は止まっていて、浮き輪は川の流れに乗って下流へ流されているので、船と浮き輪の距離はちぢまっています。 距離は 5 − 4.5 ＝ 0.5（km）ですね。これを浮き輪が15分で流れているので、流れの速さは、   |
| ＜問題3 （3）の考え方と答え＞ |
| 問（1）（2）から、次のことがわかります。 上りの速さ 10 ＋ 2 ＝ 12 → 時速12km 下りの速さ 10 − 2 ＝ 8 → 時速 8km 船は30分かけてA地からB地に進んだので、その距離は、  よって、往復にかかる時間は？ （A地→B地）＋（休み）＋（B地→A地） を計算すればいいんですね。   |
