算数「速さ(旅人算・通過算)」[中学受験]
お気に入りに登録
どの教科・単元にもいえることですが、「速さ」の単元も、攻略のカギはまず基本をおさえること。公式をしっかりと覚え、さまざまな問題にくり返し取り組むこと。問題文をよく読み、どの公式を当てはめることができるかを読み解く力を養うことで、「答えを導き出すための考え方」を身につけることができます。
今回もツカム先生といっしょに、楽しみながら学習していきましょう。

■算数「速さ(旅人算・通過算)」
こんにちは、合格総理大臣ミスター・ツカムです。
「速さ」の単元はいくつかの種類に分かれて問題があります。
例えば、旅人算・通過算・時計算・流水算・速さと比・速さのつるかめ算…などです。
「ええっ! そんなにあるの?」って、おどろかないでくださいね。基本をしっかりおさえておいたら大丈夫(だいじょうぶ)です。わかりやすいように図にかいて整理してみますね。
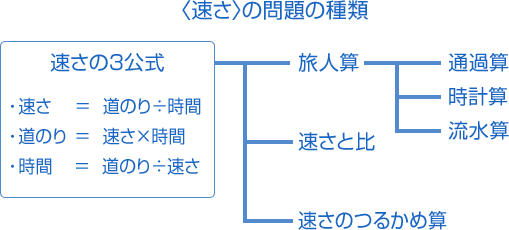
このような関係になっていますよ。
まず、「速さの3公式」を完ぺきに定着させること。それから、「旅人算」が定着していないと、「通過算」「時計算」「流水算」は理解できない…ということなんです。
おどかしているわけじゃあ、ありませんよ。逆に言えば、「旅人算」がしっかり理解できれば、「通過算」「時計算」「流水算」はおそれることはない! …です。
それでは、今回も入試問題を考えながらしっかりマスターして、この単元をキミのモノにしてくださいね。
| 問題1 |
| 池のまわりに1周4kmの道があります。この道を、A、B、Cの3人がAとBは同じ向き、Cは2人と逆向きに、それぞれ一定の速さで走っています。Aは分速250mで走っていて、AはBに40分ごとに追いぬかれ、AとCは10分ごとに出会います。 このとき、次の問いに答えなさい。 (1)B、Cの分速をそれぞれ求めなさい。 B(分速 m) C(分速 m) (2)BとCは何分ごとに出会いますか。( 分) (大阪桐蔭中 2008年 ユニーク入試) |
| <問題1の考え方と答え> |
| 旅人算の問題のパターンに、池や遊歩道のような「周」を回るものと、ある区間を往復する…という2つがあります。入試には頻繁(ひんぱん)に出題されています。 この機会にぜひマスターしてくださいね。 |
| (1)の考え方と答え |
| この問題は周を回る問題です。 図はそのまま円形でかいてもいいですが、進む道のりを一直線に表すと考えやすくなります。 速さの問題では、図をかくことが問題を解くうえでとても重要ですよ。 こんなふうにかいてみます。 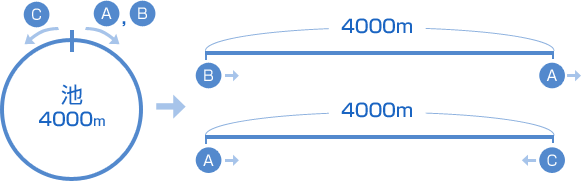 どうでしょう? 全くの基本形になりましたよね? あとは簡単(かんたん)です。 Bは4000mの道のりを、A(分速250m)に40分で追いつきます。 2人は同じ向きに走っているので、2人の速さの差は、 4000 ÷ 40 = 100 Bの速さは、Aの速さより分速100m速いから、 250 + 100 = 350 → Bは分速350m また、Bの速さを分速□mとして、次のような式を立ててもいいですよ。  4000 ÷ 40 = □ − 250 □ = 350 次に、CとAは4000mの道のりを、10分で出会います。 2人は逆向きに走っているから、2人の速さの差の和は、 4000 ÷ 10 = 400 つまり、Cの速さは、 400 − 250 = 150 → Cは分速150m また、Cの速さを分速□mとして式を立てるなら、次のようになります。  4000 ÷ 10 = 250 + □ □ = 150 |
| <(2)の考え方と答え> |
| 4000mの道のりを、Bは分速350m、Cは分速150mで逆向きに走るので、 4000mを分速(350 + 150)mで進んだときの時間を求めると、  |
| 問題2 |
| A駅、B駅間を往復している大型バスとマイクロバスがあります。A駅からは大型バスが、B駅からはマイクロバスが7時に同時に出発しました。出発して17分後に、A駅から17km離(はな)れた地点でこの2台は初めてすれちがいました。また、2度目にすれちがったのはA駅から8.5km離れた地点でした。 (1)2度目にすれちがったのは何時何分ですか。 (2)A駅、B駅間は何kmありますか。 (3)マイクロバスの速さは時速何kmですか。 (芝浦工業大学柏中 2008年 小問一部略) |
| <問題2の考え方と答え> |
| さて今度は、ある区間を往復するパターンですよ。 このパターンは、図のかき方を覚えたら、あんがい簡単(かんたん)に解けちゃいますよ。 初めての人は何度も自分でかいてみてくださいね。 |
| <(1)の考え方と答え> |
2度目にすれちがうところまで図にしてみましょう。こうなります。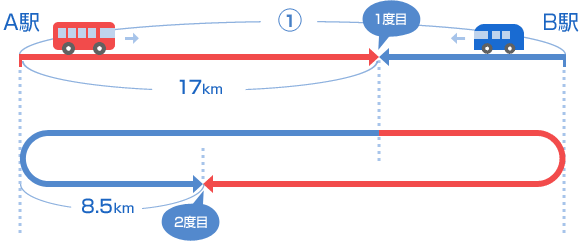  そうですね。大型バスとマイクロバスの「速さの和」のまま進むのですから、 道のりが2倍になれば、かかる時間も2倍で、 17 × 2 = 34(分) かかります。 7時に出発してから2度目にすれちがうまでの時間は、 17 + 34 = 51(分) です。 |
| <(2)の考え方と答え> |
| 大型バスは、17kmを17分で進んだので、速さは? 2度目にすれちがうまでに51分進みました。このときの道のりは? 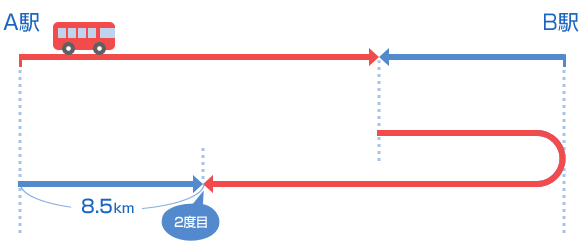 あと8.5kmたせば、A駅、B駅間の道のりの2倍になりますよね。だからA駅、B駅間は? (51 + 8.5)÷ 2 = 29.75(km) |
| <(3)の考え方と答え> |
もう一度、2台が2度目にすれちがうところまでの図を見てみましょう。 上の図の、青線の部分の道のりは? 29.75 + 8.5 = 38.25(km) ですね。 2度目にすれちがうまでに51分かかったので、 |













![算数「速さ(旅人算・通過算)」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu14/01.gif)








