算数｢速さ（旅人算・通過算）｣［中学受験］
| 問題3 |
| 2.7km離れたA、B、2地点間を関君は分速120mで往復を繰（く）り返しています。同じところを西君は分速60mで歩いていますが、関君と出会うたびに、西君は進行方向を180度変えます。今、二人同時にA地点を出発したとすると、二人が3度目に出会うのはA地点から何kmの地点でしょう。 （関西学院中 2008年） |
| ＜問題3の考え方と答え＞ |
| この問題もある区間を往復します。ただし出会った一方が方向転換（てんかん）しますね。 これも3度目に出会うまでの図を正確にかいてみましょう。こうなりますね。 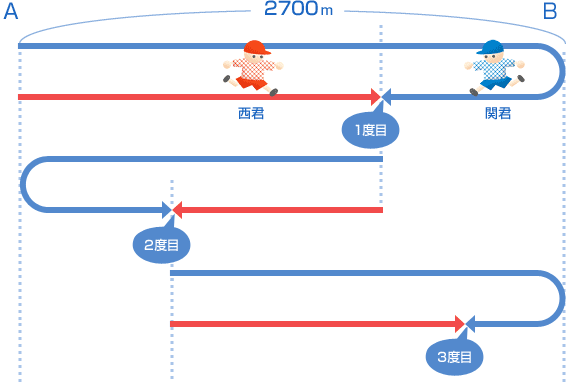 1度目の出会いから順を追って見ていきましょう。 1度目は、「2人の速さの和」の速さで進んだとき、つまり 2700 × 2 ＝ 5400（m） の道のりを進んだ地点で出会います。 このときかかった時間は、 5400 ÷（120 ＋ 60）＝ 30（分後） A地点から出会った地点までの道のりは、西君が進んだ道のりと等しいので、 60 × 30 ＝ 1800（m） → A地点から1800m のところです。 2度目。 1800 × 2 ＝ 3600（m） の道のりを進んだ地点で出会います。 3600 ÷（120 ＋ 60）＝ 20（分後） 場所は、A地点から1800mのところから、西君が1度目から2度目に進んだ道のりをひいたところなので、 1800 − 60 × 20 ＝ 600（m） のところです。 3度目。  （2700 − 600）× 2 ＝ 4200（m） の道のりを進んだ地点で出会います。  これは、A地点から600mのところで、西君が2度目から3度目に進んだ道のりをたしたところなので、   |
