算数｢速さ（流水算・時計算）｣［中学受験］
「流水算」は船が川を下ったり上ったりするときの速さ・道のり・時間について考える問題、「時計算」は時計の長針と短針によってつくられる角度を求める問題です。慣れないうちは混乱（こんらん）しやすいですが、基本となる考え方や公式が理解できれば必ずコツがつかめます。
ツカム先生がわかりやすく解説していきます。前回の「旅人算」「通過算」と合わせてくり返し取り組み、「速さ」を得意単元にしていきましょう。
■算数｢速さ（流水算・時計算）｣
こんにちは。合格総理大臣 ミスター・ツカムです。
今回は、流水算と時計算を取り上げます。
この機会にしっかりマスターして得意単元にしてくださいね。では、いっしょに学習していきましょう。
まずは流水算から見ていきましょう。
この単元でおさえるべきことは、以下の基本公式です。これをまずしっかり頭に入れてください。
上りの速さ ＝ 船の静水時の速さ − 川の流れの速さ
下りの速さ ＝ 船の静水時の速さ ＋ 川の流れの速さ
船の静水時の速さ ＝（上りの速さ ＋ 下りの速さ）÷ 2
| 問題1 |
| ある船の静水での速さは毎時20kmです。この船で、川下のA地から54km離（はな）れた川上のB地まで上るのに3時間かかりました。静水での速さを1.4倍にすると、B地からA地へ下るのに何時間何分かかりますか。 （明治大学付属明治中 2007年） |
| ＜問題1の考え方と答え＞ |
| これは基本中の基本の問題ですね。これをしっかり解くことによって、公式の意味を理解してください。 川下のA地から川上のB地まで、54km上るのに3時間かかったので、船が上っているときの速さは？ 54 ÷ 3 ＝ 18 → 時速18km です。 船の静水時の速さは 時速20kmでしたから、川の流れの速さは？ 基本公式 上りの速さ ＝ 船の静水時の速さ − 川の流れの速さ より 20 − 18 ＝ 2 → 時速2km ですね。 次に、船の静水時での速さを1.4倍にすると、 20 × 1.4 ＝ 28 → 時速28km となり、 下りの速さは、川の流れの速さを加えた速さなので、 28 ＋ 2 ＝ 30 → 時速30km よって、B地からA地に下るのは、 54 ÷ 30 ＝ 1.8（時間）  |
| 問題2 |
川の下流にあるP地点と上流にあるQ地点の間を、静水時（水の流れがなく静止している）には同じ速さの2つの定期船A、Bが往復しています。AはP地点を、BはQ地点を同時に8時に出発します。下のグラフはこの定期船A、Bの運行の様子（ようす）を表しています。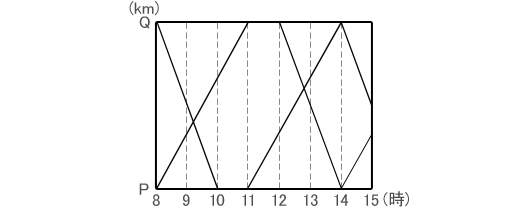 （1）静水時の定期船の速さは、川の流れの速さの何倍ですか。 （2）AとBが最初に出会ってから次に出会うまで何時間何分かかりますか。 （東邦大学付属東邦中 2008年） |
| ＜問題2の考え方と答え＞ | ||
| 次は、ダイヤグラム（運行表）を正確に読んで考えていく問題です。 | ||
| ＜（1）の考え方と答え＞ | ||
| まずグラフから、上りにかかる時間と下りにかかる時間を読み取りましょう。 上りは → 3時間 下りは → 2時間 ですね。 わかっているのはこれだけですよね？ 手がかりがないので、それぞれの速さを比で表してみます。 「かかる時間」と「速さ」は逆比の関係ですから、
基本公式は 船の静水時の速さ ＝（上りの速さ ＋下りの速さ）÷ 2 でしたから、  すると、川の流れの速さは？ 基本公式 上りの速さ ＝ 船の静水時の速さ − 川の流れの速さ より  よって、静水時の定期船の速さが、川の流れの速さの何倍かは、次のように求めることができます。   | ||
| ＜（2）の考え方と答え＞ | ||
| 小問（1）で求めた速さを使って地道に計算してみます。 ・1回目の出会いの時刻（じこく）は？  1回目に出会う時刻は → 9時12分 ですね。 ・2回目の出会いの時刻は？   2回目に出会う時刻は → 12時48分 ですね。 求めるのは、AとBが最初に出会ってから次に出会うまでにかかった時間ですから、 12時48分 − 9時12分 ＝ 3時間36分  | ||
| ＜（2）の別解＞ | ||
ダイヤグラムの図形の相似に注目してもいいですよ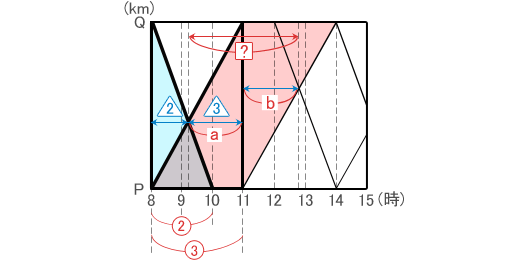！   このとき、a の部分の時間は、 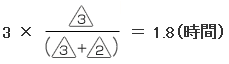 同じように、11時から14時までの3時間を見て、b の部分の時間は、a と同じ1.8時間なので、 1.8 × 2 ＝ 3.6（時間）  |
