算数「速さと比（１）」［中学受験］
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題3 |
| ある池の周りをA君とB君は同じ方向に、C君は逆方向に，それぞれ一定の速さで回ります。A君はB君を15分ごとに追いこし、B君はC君と2分ごとに出会います。B君が7分かかって走る距離（きょり）をC君は8分で走ります。このとき、A君とC君の速さの比を求めなさい。 （麻布中 2007年） |
| ＜考え方と答え＞ |
こういう「池の周り」とか「円周」をぐるぐる回るものは、直線の線分図をかくとわかりやすい人もいるかもね。図にかいてみましょう。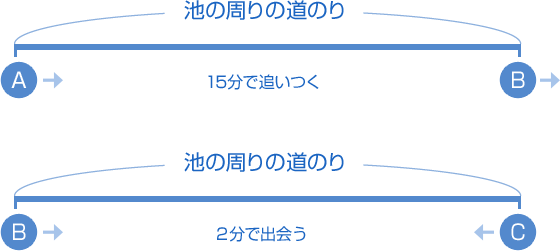 A君はいずれB君に追いつくので、池の周り1周分、うしろからスタートすると考えればいいね。この２つの図で、「旅人算の基本2パターン」が明確になったよね？ ではまず、わかっている比から求めよう。 「B君が7分かかって走る道のりをC君は8分で走ります」…から2人の速さの比は？ 時間の比は 7：8 で、速さは「逆比」になるから、  次に、下のほうの図に注目すれば、B君とC君は2分で出会うのですから、池の周りの道のりを□で表せることに気づきます。 道のり ＝ 速さ × 時間 だから、  ここまできたら旅人算の基本ですね。  A君の速さを□とすると、 速さ ＝ 道のり ÷ 時間 で、  |
関連するおすすめの記事
