算数「速さと比(1)」[中学受験]
お気に入りに登録
実際の入試問題をご覧になると、実にさまざまな問題があることに驚かれると思います。とくに算数では、複数の単元の要素を組み合わせた問題も多く、一見すると難問ばかりと思えるかもしれません。しかし算数は、基本をしっかりと理解し、繰り返し問題に取り組むことで、「答えを導き出すための考え方」を身につけることができる教科です。
■「速さと比(1)」
速さと比で、まずおさえておくことといえば?
速さが一定のとき → かかる時間の比 と 進む道のりの比 は等しい
時間が一定のとき → 速さの比 と 進む道のりの比 は等しい
道のりが一定のとき → 速さの比 と かかる時間の比 は「逆比」になる
…ということでしたね。大丈夫ですね?
「なんか、ゴチャゴチャ言ってるなあ」と思ったきみ、実際に問題を解いていけば、とっても簡単なことだよ。 基本的な問題から入試問題までいっしょにチャレンジしていこうね。この「速さと比」、3回シリーズが終わるころには、きみの大得意単元になるはず。
では、いってみましょう!
| 問題1 |
| 晴天のある日、イチローくんはメジャーリーグの野球の試合を観戦するために、家からスタジアムに向かいました。 結局、家を出てから15分後にスタジアムに着きました。「よかったー」 1.イチローくんが分速60mで歩いた時間は何分ですか? |
| <考え方と答え> |
| ではまず、図をかいて整理してみましょう。わかっている比をすべて書き出すことが大事。 名探偵でも、まず事件でわかっていることをすべて整理することから始めるよ。 きみも「算数の名探偵」になったつもりでね。 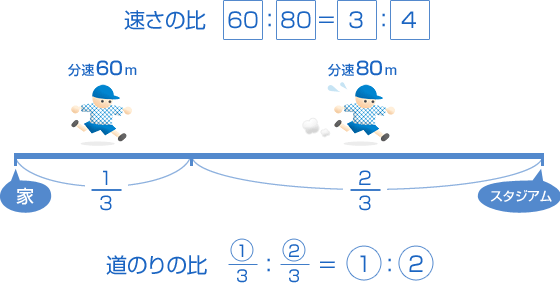 ここで注意することは、「道のりの比」は○で表し、速さの比は□というように、自分で決めておくこと。 3つつなげると ○‐□‐△‐ となって、おでんの形に似ているから、ミスター・ツカムはこれを「おでん解法」と言っているよ。 あとは、かかった時間の比がわかれば、問題を解く手がかりはすべてそろうよ! 速さの3公式のとおりに計算すればいいんだよ。 時間=道のり÷速さ だから |
| <1の答え> |
家からスタジアムまで15分かかったので、最初分速60mで歩いていた時間は? |
| <2の答え> |
| 分速60mで6分歩き、分速80mで9分進んだので、家からスタジアムまでの道のりは? 1の答えから、分速80mで歩いた時間は 15-6=9 で、9分だとわかるね。 道のり = 速さ × 時間 だから、 どうです? メッチャ簡単でしょ? 続いて基本的な問題でしっかり定着させましょう。次もワクワク文章題でいくよ。 |
| 問題2 |
| イチローくんとシンジョーくんが100m競走をしました。足の速い2人の対決はとっても楽しみです。イチローくんがゴールしたとき、シンジョーくんはかみ形を気にしながら走っていたので、ゴールまであと12mの地点にいました。 また、シンジョーくんはイチローくんより2.4秒遅れてゴールしました。 カッコつけるな! シンジョーくん。 1.イチローくんとシンジョーくんの速さの比は? 2.イチローくんは100m走るのに何秒かかりましたか? |
| <考え方と答え> |
さあ、さっきと同じように、わかっていることを図にかいてみましょう。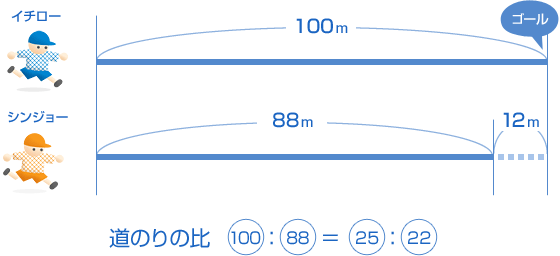 |
| <1の答え> |
 |
| <2の答え> |
次に、2人それぞれがかかった時間の比を求めます。 それで、2人の時間の差が2.4秒でした。  ここでのポイントは、○ や △ や □ を具体的な数と結びつけるということです。 |
関連するおすすめの記事













![算数「速さと比(1)」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/432/080610_q1_1.gif)








