算数｢ともなって変わる量・水量の変化｣［中学受験］

中学受験

歯車の回転について考える問題や、水量の変化する様子をグラフから読み解く問題など、状態の変化をイメージする力が求められる良問を、全国の中学入試問題から集めました。理解を深めるために自分でも図やグラフをかいて、じっくり、くり返し取り組みましょう。グラフを読む力は、ほかの多くの算数単元や理科でも大きな強みとなります。
今回もツカム先生がわかりやすく解説していきます。楽しみながら取り組んでいきましょう。

■算数「ともなって変わる量・水量の変化」

こんにちは。合格総理大臣ミスター・ツカムです。
今回は「ともなって変わる量・水量の変化」を取り上げます。特に「水量の変化」は、多くの中学校の入試問題に取り上げられています。
ここでのポイントは、水が入っていって容器の中の水の高さが変わっていく様子と、それを表しているグラフとが、アタマの中でぴったりと一致（いっち）するかどうかです。
問題文に図やグラフがかかれていないものもあります。そういった場合は自分でかいてみる習慣をつけることが大事です。
では、さっそくミスター・ツカムといっしょに解いていきましょう。

問題1

図のように、3つの歯車A、B、Cがかみ合っています。Aの歯の数は48で、Cの歯の数は36です。また、歯車Aが1回転すると、歯車Bは3回転します。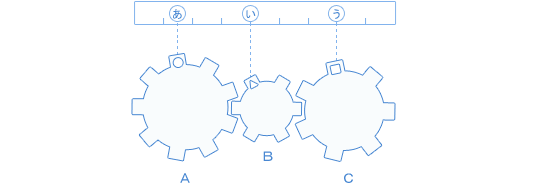

（1）歯車Bの歯の数はいくつですか。

（関西大学第一中　2008年）

＜問題1　（1）の考え方と答え＞

歯車A（歯の数 48）が1回転すると、歯車Bは3回転します。
つまり、歯車Aの歯が48個動くと、歯車Bは3回転するので、

　　　　　 48 ÷ 3 ＝ 16

＜問題1　（2）の考え方と答え＞

小問（1）より、Bは3回転して元の位置にもどるからです。

だから、歯車Aと歯車Cのしるしの位置関係だけを考えればよいことになります。

　　　　Aの歯の数＝ 48、　Cの歯の数＝ 36

かみ合う歯の数が、歯車Aの歯の数48と、歯車Cの歯の数36の倍数であれば、
AもCも元の位置にもどりますね。
つまり、この2つの歯車の歯の数の、最小公倍数を求めればよいですね。

　　　　48と36の最小公倍数　→　144

歯車Aは何回転しましたか？

　　　　144 ÷ 48 ＝ 3

問題2

図1のようにたて60cm、横100cm、高さ20cmの直方体の形をした水そうの底に、たて60cm、横20cmの直方体の形をした石を入れました。この水そうに毎分4リットルの割合で蛇口（じゃぐち）から水を入れたときの、時間と水の深さ（最も深い部分）の関係が図2です。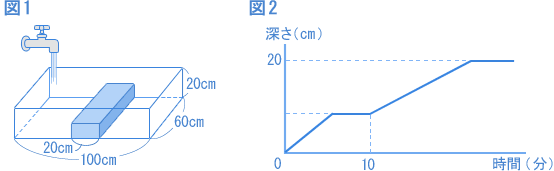

（1）石の高さは何cmですか。
（2）水そうがいっぱいになるのは水を入れ始めてから何分後ですか。

（智辯学園和歌山中　2007年）

＜問題2の考え方と答え＞

ここから水量の変化の問題です。
グラフの変化している箇所（かしょ）が、どんな状態であるのかをしっかり考えて、グラフを読み取っていきましょうね。

＜（1）の考え方と答え＞

グラフから、10分後に水が石の高さまで入ったことがわかりますね。
毎分4リットルで10分入れたときの水の量は、

　　　　4000 × 10 ＝ 40000（cm³）

これは、石をのぞいた体積と等しいので、

　　　　60 ×（100 − 20）× 石の高さ＝ 40000

　　　　　　　　　　　　　　　　