算数｢ともなって変わる量・水量の変化｣［中学受験］
| 問題4 |
図1のように、高さ25cmの直方体の水そうと、三角柱のつみ木Aとつみ木Bがあります。つみ木Aは高さ10cmで、つみ木Bは高さ20cmです。図2のグラフは、この水そうにつみ木Aとつみ木Bを1つずつ置き、毎秒50cm³ の割合で水を入れたときの時間と水面の高さの関係を表したものです。ただし、水を入れてもつみ木は水そうの底からはなれないものとし、つみ木は三角形の面を底にして水そうに直接置くものとします。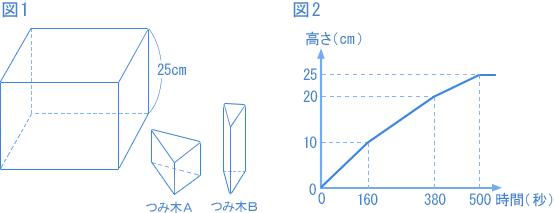 （1）水そうの底面積は何cm² ですか。 （2）つみ木Aとつみ木Bの底面積の比をもっとも簡単な整数の比で表しなさい。 （実践女子学園中 2008年 2回、1問略） |
| ＜問題4 （1）の考え方と答え＞ |
| つみ木Ａもつみ木Ｂも完全に水にうもれてからの時間帯に注目しましょう。 グラフは3段階になっています。 つみ木A、Bが水にうもれたのは、最後の380～500秒の間ですね。 120秒間で高さは、25 − 20 ＝ 5（cm）上昇（じょうしょう）しています。 よって、水そうの底面積は 50 × 120 ÷ 5 ＝ 1200（cm²）  |
| ＜問題4 （2）の考え方と答え＞ |
水が入っていく様子を、正面から見た図で表してみます。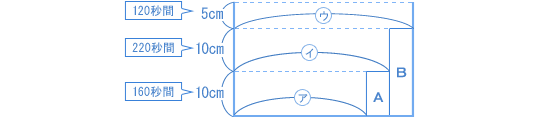 水は一定の割合で入っていきますから、入れた時間（秒）の比が、体積の比であると考えます。 底面からの体積比は 160：220：120 です。 次に、それぞれの底面積の比を求めると、 （160 ÷ 10）：（220 ÷ 10）：（120 ÷ 5）＝ 8：11：12 となりました。 したがって、AとBの底面積の比は？  ＝ 3：1  |
