算数｢ともなって変わる量・水量の変化｣［中学受験］
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題3 |
図1のような容器があります。この容器に常に一定の割合で水を入れました。そのときの時間と、底面Pから測った水面の高さとの関係を表したものが図2です。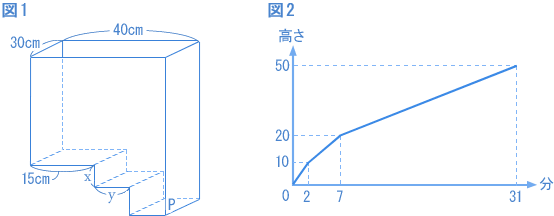 （1）ｘの長さは何cmですか。 （2）ｙの長さは何cmですか。 （栄東中 2007年） |
| ＜問題3 （1）の考え方と答え＞ |
図１に高さ「z」をつけ加えます。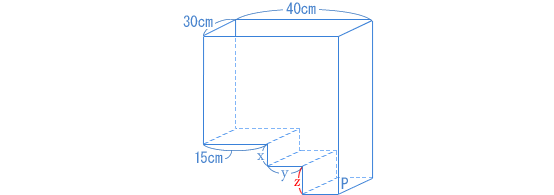 図2のグラフから、最初の10cmは「z」の長さで、次の10cmが求める「ｘ」の長さだとわかります。  |
| ＜問題3 （2）の考え方と答え＞ |
| 水を入れ始めてから高さが20cmのところまでに注目します。 正面から見ると次のような図になります。 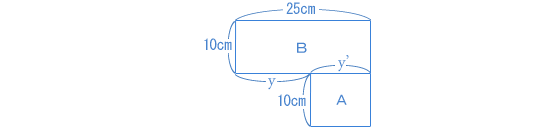 Aの部分（高さ10cm）が水でいっぱいになるのにかかる時間は、 → 2分 です。 Bの部分（高さ10cm）が水でいっぱいになるのにかかる時間は、 → 7 − 2 ＝ 5（分） です。 水は一定の割合で入っているので、入れた時間（分）の比が体積比であると考えます。 AとBの体積比は 2：5 になり、面積比も 2：5 です。 AとBの面積のたてが10cmで同じなので、y’の長さとBの横の長さ25cmの比も 2：5 です。 よって、求めるyの長さは、   |
