算数｢ともなって変わる量・水量の変化｣［中学受験］
| 問題5 |
| 側面に小さな穴が一つあいた水そうが置かれていて、水面が穴より上にあれば、穴から水が流れ出ます。空（から）の状態からこの水そうに毎分30リットルの量の水を注ぎました。穴から水が流れ出ても注ぎつづけると、水位は上昇（じょうしょう）したので、満水になったところで注水を止めました。注水を止めてから、穴から水が流れ出なくなるまでに21分かかりました。穴から流れ出る水の量はいつも一定で、流れ出た水の総量が180リットルであるとき、 （1）穴から水が流れ出始めてから何リットルの水を注ぎましたか。 （2）穴から水が流れ出始めてから流れ出なくなるまでに何分かかりましたか。 （3）この水そうの穴から上の部分の容積は何リットルですか。 （開明中 2008年 後期） |
| ＜問題5の考え方と答え＞ |
| こういう文章だけで、図やグラフが示されていない問題は、自分で簡単（かんたん）にかいてみましょう。 そのほうが考えやすくなりますよ。 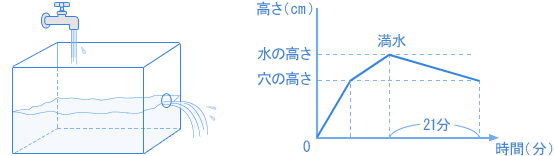 これで考えやすくなりましたよね？ |
| ＜（1）の考え方と答え＞ |
| これは落ち着いて考えれば答えは簡単ですよ。 「穴から水が流れ出始めて」から、あとどれだけ水を注いでも、全部流れ出てしまいますよ。 つまり、流れ出た水の総量が答えです。  |
| ＜（2）の考え方と答え＞ |
 これが、求める時間です。 ［イ］は21分とわかっていますから、［ア］を求めましょう。 小問（1）で、穴から水が流れ出始めてから注いだ水の量は180リットルと求めているので、 180 ÷ 30 ＝ 6（分間） です。 ですから、 6 ＋ 21 ＝ 27（分間）  |
| （3）の考え方と答え |
| 上で求めたように、180リットルが流れ出るまでに27分間かかっています。 そのうちの21分間は、穴から上の部分の水が外に出た時間ですね。 ですから上の部分の容積は、   |
いかがでしたか？
水量の変化は、まずグラフのそれぞれの箇所（かしょ）がどんな状態なのか？ …をしっかり理解することです。何度も演習して自分のものにしてくださいね。
今回「比例・反比例」の問題を解くにあたって、「比・逆比」の発想も大切だと気づきましたね？
この考えをふまえて、「比例・反比例」を復習しましょう。
合格総理大臣 ミスター・ツカム
