算数｢平面図形と比（1）｣［中学受験］
中学受験カウンセラーのミスター・ツカム氏が、実際の入試問題の解き方・考え方をていねいに解説していきますから、いっしょに取り組んでいきましょう。
■算数｢平面図形と比（1）｣
こんにちは。ミスター・ツカムです。「平面図形と比」を取り上げますよ。この単元も受験算数では重要単元。
どの学校も出題頻度（ひんど）が高いですから、しっかりと理解を深めてください。
入試問題を考えていく前に、「底辺比と面積比」の基礎知識（きそちしき）を確認（かくにん）していきましょう。
まずは基本形から。
《キホン-1》
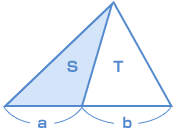 | 左の大きな三角形で、面積 S、T の比は？ S ： T ＝ a ： b になりますよね。 高さが同じだから、底辺比＝面積比 になります。 簡単（かんたん）ですよね？ |
では、次のパターン。
《キホン-2》
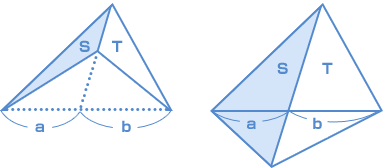 | いずれも、 S ： T ＝ a ： b になります。 だいじょうぶですね？ |
その他、「底辺比＝面積比」の応用でこんなのもありますね。
《キホン-3》
以上を確認したうえで、入試問題を考えていきましょう。
| 問題1 |
三角形ABCの辺ABを2等分、辺BCを3等分、辺CAを4等分し、点D、E、Fを決めます。このとき、内部にできる三角形をPQRとします。また、CR ： RP ： PD＝2 ： 2 ： 1、BQ ： QR ： RF＝2 ： 2 ： 1とします。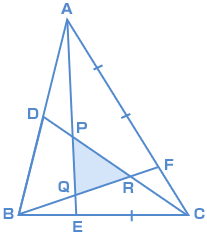 （1）三角形ABCの面積は三角形ABEの面積の何倍ですか。 （2）三角形ABCの面積は三角形PQRの面積の何倍ですか。 （東海大学付属浦安高等学校中等部 2007年・B試験） |
| ＜問題1 （1）の考え方と答え＞ |
| これは基本中の基本ですね。 底辺比 BE ： BC ＝ 1 ： 3 だから、 三角形ABE と 三角形ABC の面積比も 1 ： 3 になります。  |
| ＜問題1 （2）の考え方と答え＞ |
| いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形PQR の辺の延長線上で、比がわかっている BQ ： QR ： RF ＝ 2 ： 2 ： 1 に注目します。  次に、CR ： RP ： PD ＝ 2 ： 2 ： 1 に注目して、    底辺比を着実に確認していけば、面積比は必ず求められますから、自分で図に比を書きこんで、早く慣れるようにしましょうね。 |
