算数｢平面図形と比（1）｣［中学受験］
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題2 |
| 図のような平行四辺形ABCDがあり、点E、Fはそれぞれ辺CD、ADの真ん中の点です。このとき、 斜線（しゃせん）部分の面積は平行四辺形の面積の何倍ですか。 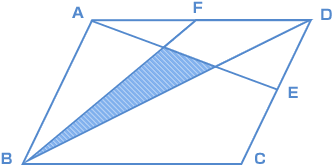 （海城中 2007年・2回） |
| ＜問題2の考え方と答え＞ |
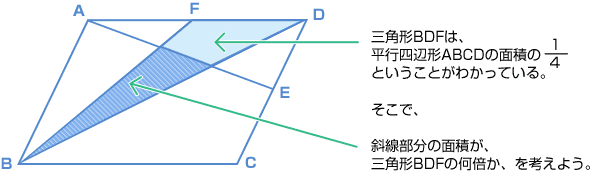  次に、斜線の部分の面積を表しやすいように、点G と H をつけておきます。 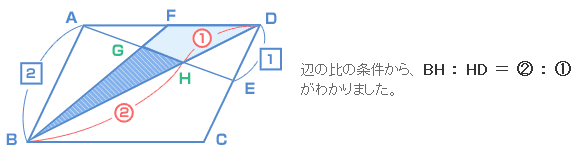 ここでもし、BG ： GF の比がわかれば、最初に確認した《キホン‐3》の法則が使えますよね？ 補助線（ほじょせん）をひいてみたら、次のように比がわかりました。 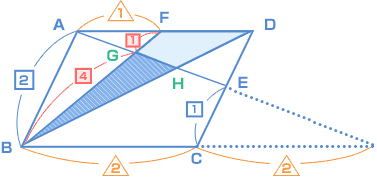  最後に整理して図にかくとこうなりました。 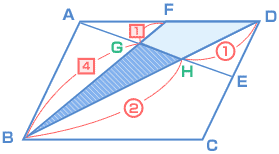 だから、三角形BHG の面積と 三角形BDF の面積の比は？ ( 4 × 2 ) ： ( 5 × 3 ) ＝ 8 ： 15 となり、    どうでしたか？ 少し難（むずか）しかったですか？ 最初から、補助線をひいたりするアイデアを思いつくのはなかなか難しいと思うけど、何度も問題を解いていると、ふと思いつくんですよ。だからくり返し練習することと、数を多くこなすことです。 |
