算数｢平面図形と比（1）｣［中学受験］

問題4

図のような三角形ABC、DEF、GHIがある。点D、E、Fは三角形ABCの辺の延長上にそれぞれAB：BD＝1：2、BC：CE＝1：1、CA：AF＝1：3となる点である。また、辺GH、HI、IGはそれぞれ点Fを通りABに平行、点Dを通りBCに平行、点Eを通りCAに平行である。 （1）三角形DEFの面積は三角形ABCの面積の何倍ですか。 （2）斜線部分の面積の和は三角形ABCの面積の何倍ですか。 （金蘭千里中　2008年）

＜問題4　（1）の考え方と答え＞

まず、三角形DEF について図をかき出してみましょう。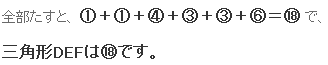

＜問題4　（2）の考え方と答え＞

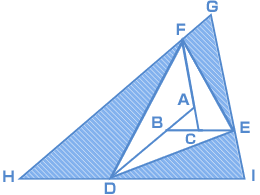
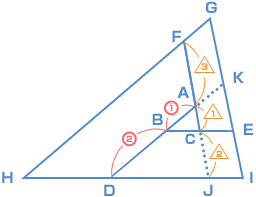
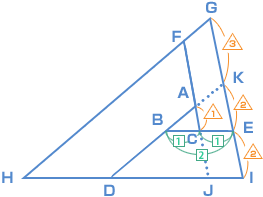
考え方としては、（1）で三角形DEFの面積が三角形ABCの何倍かわかったので、三角形GHIが三角形ABCの何倍か？…を求めればいいということですね。 問題文の中の、「点○を通り、……に平行」という条件をまだ使っていないので、ここにヒントがあるのかも？　と当たりをつけて図をかいていきます。 AC と BA それぞれの延長線上に、次のように点J と 点K を付け加えます。 GH、HI、IG はAB、BC、CA にそれぞれ平行だから、 四角形AKGF と 四角形CJIE は平行四辺形になっています。 だから、 次に、三角形ABC と 三角形KBE は相似で、 BC ： CE ＝ 1 ： 1 なので、EKの長さは となりました。 三角形GHI は 三角形ABC を7倍に拡大（かくだい）したことになります。 ということは、面積比は？ 三角形ABC ： 三角形GHI ＝ ( 1 × 1 ) ： ( 7 × 7 ) ＝ 1 ： 49 三角形GHI の面積は、三角形ABC の49倍です。 三角形DEF の面積は、三角形ABC の18倍でしたから、 斜線部分の面積は、 49 — 18 ＝ 31

以上です。
4つの問題を取り上げましたが、どうでしょうか？ 難しいと感じましたか？ でも、「底辺比＝面積比」「相似比を見つける」ことができれば、問題は解ける…ということもわかってもらえたと思います。今後、きみが他の「平面図形と比」の問題に取り組むときは、

　　　　・「底辺比＝面積比」
　　　　・「相似比を見つける」

これらのことを最初に思い出して（問題の横に書いてもいいぐらいです）、落ち着いて考えてみてね。

合格総理大臣 ミスター・ツカムでした。