算数｢平面図形と比（1）｣［中学受験］

お気に入りに登録

問題3

右の図のような平行四辺形ABCDがあり、底辺BCの長さは14cm、高さは10cmです。また、三角形EBFの面積は20cm²です。

　　（1）三角形EFDの面積は何cm²ですか。

　　（2）AEの長さは何cmですか。

（桐朋中　2007年）

＜問題3　（1）の考え方と答え＞

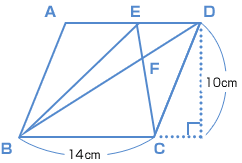
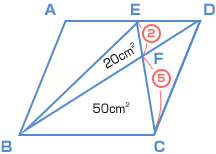
三角形EBC の面積は、14 × 10 ÷ 2 ＝ 70（cm²）で、三角形EBF の面積が20（cm²）だから、
三角形FBC の面積は？

70 — 20 ＝ 50 （cm²）

	底辺比＝面積比より、 EF ： FC ＝ 2 ： 5 であることがわかる。
	これより、三角形EFD と三角形CFB の辺の長さの比は同じであるから、 DF ： BF ＝ 2 ： 5 である。

だから、三角形EFD と三角形EBF の面積比も 2 ： 5

つまり、三角形EFD の面積は

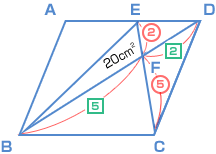
＜問題3　（2）の考え方と答え＞

ED ： CBも 2 ： 5 で、AE ： AD ＝ 3 ： 5 となる。
AD ＝ BC ＝ 14 cm だから、AEの長さは？

ミスター・ツカム

大人気メールマガジン「コロンブス的・超発想で中学受験を成功させる方法」の発行人で、中学受験カウンセラー。メルマガは殿堂入りを果たす。理科・替え歌暗記法のCD『愛のメモリーTM』も作成。

おすすめ特集