算数｢平面図形と比（2）｣［中学受験］
| 問題3 |
下の図において、BD ： DC＝5 ： 7、AP ： PD＝2 ： 1です。三角形PBDの面積が10cm²のとき、次の問いに答えなさい。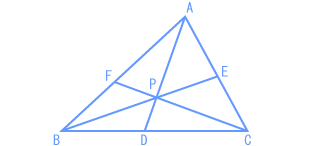 （1）三角形APBと三角形APCの面積の比を、最も簡単な整数で表しなさい。 （2）AF ： FBを、最も簡単な整数で表しなさい。 （3）三角形AFPと三角形PDCの面積の比を、最も簡単な整数で表しなさい。 （晃華学園中 2008年） |
| ＜問題3の考え方と答え＞ | ||
まずは三角形の「底辺比」と「面積比」の基本事項（じこう）を確認（かくにん）しておきましょうね。
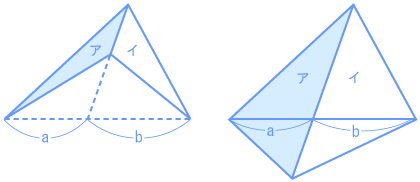
まずは基本形から。
では、次のパターン。
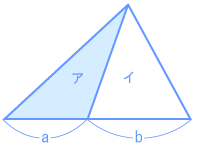
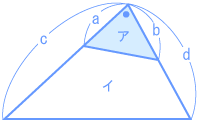
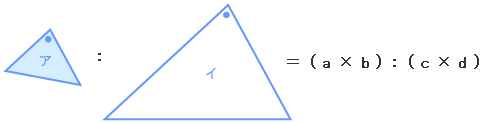
その他、「底辺比＝面積比」では、こんなのもありますね。 | ||
| ＜（1）の考え方と答え＞ | ||
| さっそく登場しましたね。これぐらいよく出てくるんですよ。 これは、上の基本事項が理解できていれば、かんたんですね。  | ||
| ＜（2）の考え方と答え＞ | ||
わかっている比や面積を図に記入します。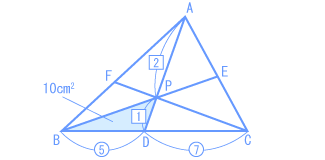 三角形APCと三角形PBCの面積比がわかれば、AF ： FB もわかりますね。 まずは三角形PDCの面積を求めます。 BD ： DC ＝ 5 ： 7 だから、  三角形APCの面積は、 AP ： PD ＝ 2 ： 1 だから、  AF ： FBは、三角形APCの面積 ： 三角形PBCの面積と等しいので、 AF ： FB ＝ （三角形APC） ： （三角形PBD ＋ 三角形PDC） ＝ 28 ： （10 ＋ 14） ＝ 28 ： 2 ＝ 7 ： 6  | ||
| ＜（3）の考え方と答え＞ | ||
小問（1）、（2）でわかったことを整理して図にかいてみます。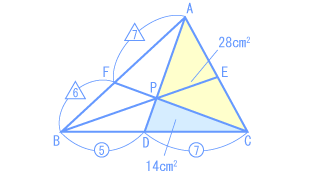 三角形AFPの面積を求めるために、まず三角形APBの面積を求めます。 三角形APB ： 三角形APC ＝ 5 ： 7 だから 三角形APBの面積は、  よって、三角形AFPの面積は、  では、求める面積比は？   |
