「速さとダイヤグラム」の解き方［中学受験］算数の頻出問題
| 問題3 |
| A君は8時に駅からテニスコートに向かって歩き出しました。B君は8時3分に駅からテニスコートに向かって歩き出しました。すると、駅からテニスコートまでのちょうど3分の1の所にあるポストの前でB君はA君を追いこし、8時39分にテニスコートに着きました。ちょうどその時、A君はテニスコートの手前216mの所にいました。 （1） A君がテニスコートに着く時刻を求めなさい。 （甲陽学院中 2007年） |
| ＜問題3の考え方と答え＞ |
| これもまずはダイヤグラムをかいてみましょう。 そして相似を見つけて相似比を書きこんでね。  |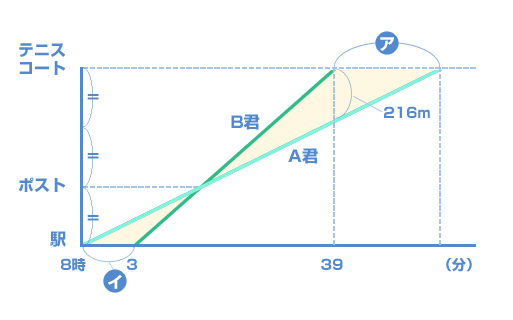
| ＜（1）の考え方と答え＞ |
| 図から、右上と左下の色付き部分の三角形は、相似比が 2：1 になっていますよね。 だから、 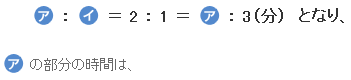 3 × 2 ＝ 6（分） です。 A君がテニスコートに着く時刻（じこく）は、 39 ＋ 6 ＝ 45（分）  |
| ＜（2）の考え方と答え＞ |
| A君かB君の歩く速さがわかれば、駅からテニスコートまでの距離（きょり）は求められますね。 さて、どちらの速さがわかりますか？ 216mはどっちに関係しているでしょう？ A君ですよね。A君は216mを6分で歩いています。 A君の速さは、 216 ÷ 6 ＝ 36 毎分36m だから求める距離は、 36 × 45 ＝ 1620  |
