「速さとダイヤグラム」の解き方［中学受験］算数の頻出問題
お気に入りに登録
アプリなら
会員登録不要で
記事を保存できます
| 問題5 | ||||||
一郎（いちろう）君はA駅から12km離（はな）れたB駅まで自転車に乗って時速18kmの速さで行きました。A駅とB駅の間は1台の電車が常に一定の速度で往復しており、2つの駅での停車時間は同じです。下のグラフはその様子を表したものです。次の問いに答えなさい。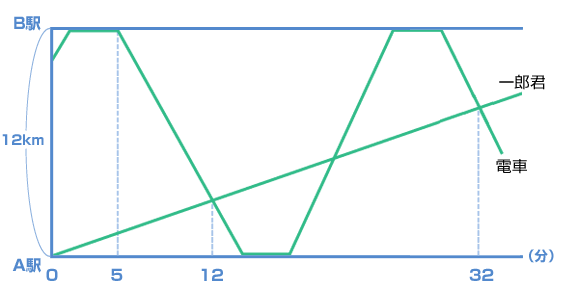
（六甲中 2008年 後期） |
| ＜問題5 （1）の考え方と答え＞ |
| ダイヤグラムから、初めに出会う地点がわかれば電車の速さが求められますね。 一郎君の自転車の分速は、 18000 ÷ 60 ＝ 300 m/分 出発して12分後に出会ったので、A駅から 300 × 12 ＝ 3600（m）の地点 電車は、（12000−3600）mの距離を（12−5）分間で走っているので 8400 ÷ 7 ＝ 1200 m /分 1200 × 60 ＝ 72000 m / 時  どうして、分速から求めて時速に直すという、めんどうなことをやったのか？ |
| ＜問題5 （2）の考え方と答え＞ |
| 電車の停止時間をつきとめるために、まずは、 一郎君が、電車と初めて出会って（12分）、次に追いつかれて、もう一度出会うまで（32分）の20分間に、電車はどれだけの距離（きょり）を進んでいるのか。図をかいて考えてみましょう。 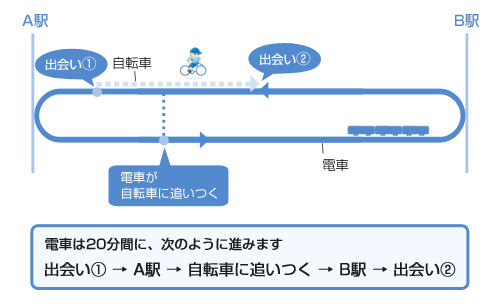 図からわかるように、12分から32分の20分間に、「A駅とB駅の間の２倍の距離」から「自転車で走った距離」をひいた距離を電車が進んだことになります。 12000 × 2 − 300 ×（32 − 12）＝ 18000（m） 電車がこの距離を進むのにかかる時間は？ 18000 ÷ 1200 ＝ 15（分） 2回の停車をふくめて 20分 かかっているので、1回の停車時間は、 （20 − 15）÷ 2 ＝ 2.5  |
| ＜問題5 （3）の考え方と答え＞ |
| 電車がA駅を出発するのは、一郎君がA駅を出発してから 5 ＋ 12000 ÷ 1200 ＋ 2.5 ＝ 17.5 分後 ですね。 一郎君は、 300 × 17.5 ＝ 5250m 先を行っています。 だから、電車が一郎君に追いつくのは、電車がA駅を出発してから   それは一郎君がA駅を出発してから何分何秒後かというと、   |
「速さとダイヤグラム」の基本は、
1. 文章を正確に読み取り、ていねいにダイヤグラムや図に表す。
2. わかった数値（すうち）を書きこんでいく。
ということですよ。
今回の5問をマスターできたら、他のダイヤグラムの問題にもチャレンジしてみてくださいね。
ミスター・ツカムでした。
