算数の文章問題、さまざまな単位が混ざった問題が理解できません[中学受験]
お気に入りに登録
平山入試研究所の小泉浩明さんが、中学受験・志望校合格を目指す親子にアドバイスする実践的なコーナーです。保護者のかたから寄せられた疑問に小泉さんが回答します。

【質問】
算数の文章問題の応用が苦手です。特に、メートルとセンチなど、さまざまな単位が混ざった問題は理解ができていないようです。どのようにすれば改善するでしょうか?
相談者:小6女子(大ざっぱ・弱気なタイプ)のお母さま
【回答】
「同じにする」「同じところ」「特別なところ」は算数の大切なポイント
■つい忘れがちな“単位をそろえる”
「メートルとセンチが混ざった問題は理解できない」ということですが、頭ではわかっていてもつい混乱してしまうのでしょう。算数では何かと何かを比べることが多いのですが、その場合は必ず単位を同じにします。単位、つまり条件を同じにしないと、比べることができないからです。こうした原則は当然のように思えますが、問題を解く段になるとつい忘れてしまいがちです。
「条件を同じにしないと比べられない」ことを実感させるためには、コップの水の量を比べる実験をよく行います。まず違う形のコップに同じ量だと思えるだけ水を注がせます。次に、同じ形のコップにそれぞれの水を移し替えてその高さを比べます。すると、同じ量だと思った水の量が、意外に違っているということに気付くという実験です。小学校の授業などで行うことも多いと思います。
■単位をそろえるクセを付けるには?
こうしたコップの実験や日常的な経験を通して、同じ条件で比べることの必要性は認識しているはずです。しかし、算数の問題を解く時に「単位を同じにする」ことをつい忘れてしまうことはあります。そうした原則を定着させるためには、文章題の応用に取りかかる前に、簡単な計算から始めて慣れていくことが大切です。
単位をそろえる計算としては、時間、分、秒の計算やリットルと立方センチメートルが混ざった計算など数多くあります。お子さまはそうした計算練習を重視せずに、あまり演習を重ねなかったのかもしれません。計算練習はくり返し行わなければ定着しませんから、そうした勉強を苦痛に感じて避ける子どもも少なくないと思います。しかし、習慣として単位をそろえられるようになるには、そうした計算演習をくり返す必要があります。そして、計算に慣れてきたら、文章題でも単位をそろえることを忘れないようになると思います。
■同じにすることの大切さ
条件をそろえる、あるいは同じにするということは、何も単位の計算だけではありません。前述のように、算数では比べるという作業が非常に重要なカギとなります。算数のさまざまな場面で、「同じにする」という考え方を使って問題を解いていきます。次の例題を見てみましょう。
例題:次郎と三郎の所持金の比は4:3でしたが、三郎が600円使ったので、
その比が2:1となりました。次郎が初めに持っていたお金はいくらですか。
〔考え方〕
次郎の所持金は変わらないので、右の図で、4と2は等しい。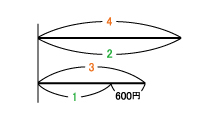 これを4にそろえると、次郎と三郎の比は、
これを4にそろえると、次郎と三郎の比は、
使う前 〔4:3〕 =4:3
使った後 〔2:1〕 =4:2
三郎の比の差3-2=1が600円にあたる。
これにより次郎の所持金は600×4=2400(円)。
倍数算の問題ですが、ここでは比を4や2で表し、それらを同じにすることで問題を解いていきます。こうした比の扱いは子どもたちがよくつまずくところの1つです。3と1は比べているものが違うので、条件を同じにしないと比べられません。こうしたことも、長さや面積の単位を同じにして比べることと原理的には同じなのです。
■「同じ」「特別」は算数の要
算数では、このように「同じにして比べる」ことが非常に大切です。そしてさらにその考え方を広げていけば、「同じところ」と「同じでないところ」すなわち「特別なところ」に注目することが、問題を解く時に大いに役立ちます。たとえば、同じところを見つけることで、二等辺三角形や正三角形を見つけ、それらの性質を使って問題を解きます。あるいは、相似形を発見できるかもしれません。また、特別なところである「直角」から直角三角形を見つけ、その性質から解法の糸口を導き出せることもあるでしょう。図形問題だけではありません。規則性の問題ではくり返し同じように現れる規則を見つけることで問題を解いていきます。また、線分図では、前述のように“どことどこが同じである”ということから立式していきます。
このように「同じにする」「同じところ」そしてその逆である「特別なところ」は算数の問題を扱ううえで重要なポイントです。具体的な説明により理解を深めると共に、演習を重ねることで定着させましょう。
みんなが読んでる!おすすめ記事
- 小学校低学年から理科に興味を持てるように!子どもに投げかけたい質問例
- 小学生になったら学校の持ち物を一人で準備できるようになってほしい 100均グッズで簡単!「忘れ物チェックボード」【おうちで知育工作】
- 社会福祉学とは? 学ぶ内容や大学選びのポイント、取得できる資格を解説
- 「上手な断り方」を身に付けさせる特別授業[こんな先生に教えてほしい]
- 「我が子に合った学校」とは、どのような学校か[中学受験]
- 淑徳大学 総合福祉学部 社会福祉学科 (1) 社会福祉士を育成しながら 現場の経験を生かして社会保障政策などを研究[大学研究室訪問]
- 人が良すぎてNOと言えない娘……断れない娘[うちの子、どう接したらいいの?]
- 不登校の子どもが「進級(進学)したら学校に行く」と言うのを信じてよい? 本当に行けるようになる?[不登校との付き合い方(19)]
- 淑徳大学 総合福祉学部 社会福祉学科 (2) 終身雇用の時代が終わりつつある今、人生を長い目で見れば、どんな企業に就職したかより、どんな知識や技術を身につけたかが大切[大学研究室訪問]














![算数の文章問題が苦手です。文章は理解できているのに計算式をつくれません[中学受験]](/_shared/img/ogp.png)








