算数｢場合の数｣［中学受験］

お気に入りに登録

中学受験

問題5

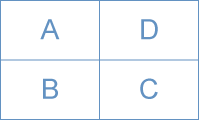右の図のようにA、B、C、Dの4つの部屋があります。使える色が4色あるとすると、この4つの部屋をぬり分ける方法は何通りありますか。ただし、全部の色を使わなくてもよく、となり合う部屋は異（こと）なる色でぬり分けることとします。

（大妻嵐山中　2008年）

＜問題5の考え方と答え＞

色をぬっていく、これも基本的な問題ですよ。
考えをまとめるために、実際に色をぬってみましょう。
例えばこんな感じですね。赤、青、黄色、緑を使ってみます。

同じ色がとなり合わなければいいので、2色でもだいじょうぶですね。
だから、ぬり方は、2色、3色、4色となります。

●［図1］のように、2色でぬる場合
AとC、BとDが、それぞれ同じ色になりますね。
AとCにぬる色は4通りなので、BとDは残りの3通り。

　　　4 × 3 ＝ 12（通り）

●［図2］のように、3色でぬる場合
AとCか、BとDが同じ色。
AとCが同じ色のとき、ここにぬるのは4通り。
Bは3通り、Dは2通りで、

　　　4 × 3 × 2 ＝ 24（通り）

BとDが同じ色のときも考え方は同じで、24通り。
だから、　3色でぬる場合は、

　　　24 × 2 ＝ 48（通り）

●［図3］のように、4色でぬる場合
A、B、C、Dの順に色を決めていきます。
（どんな順で決めていってもいいよ。答えは同じになります）
Aは4通り、Bは3通り、Cは2通り、Dは1通りだから、

　　　4 × 3 × 2 × 1 ＝ 24（通り）

合計で、

　　　12 ＋ 48 ＋ 24 ＝ 84（通り）

いかがでしたか？
初めに言いましたように、「場合の数」の単元では、しっかりと筋道（すじみち）を立てて、問題を整理して考えていくことが大事ですね。

その基礎（きそ）となるのが「樹形図（じゅけいず）」です。
これをおさえておかないと応用問題も解けませんので、必ず定着させておくようにね。

それと、実際の入試問題では、今回の【問題2】や【問題3】のように、
求めようとする場合の逆を考えて解いていく問題も多く出題されます。
このパターンも練習して身につけてください。

合格総理大臣　ミスター・ツカム