算数「場合の数」[中学受験]
お気に入りに登録
慣れないうちはむずかしく感じるかもしれませんが、あわてず、じっくりと取り組むことで、考え方・解き方を身につけることができます。オリジナル問題から実際の入試問題まで、今回もツカム先生がていねいに解説していきます。理解を深めて、得意単元を増やしていきましょう。
■算数「場合の数」
今回は「場合の数」です。この単元はどちらかというと「筋道(すじみち)を立てて考える」単元だと思います。
図形などの単元は「ヒラメいた!」…という算数のセンスがいるかもしれません。
でも、「場合の数」はていねいに筋道を立てて考えていきます。
だから、しっかりと基本を身につけること。「樹形図(じゅけいず)」は必ずかくようにしてくださいね。
では、さっそく問題にいってみましょう。
| 問題1 | ||||
| 「0」「2」「3」「4」と書かれた4種類のカードがたくさんあります。 以下の問いに答えましょう。
(ツカム先生 オリジナル問題) |
| <問題1(1)の考え方と答え> |
| それでは、「場合の数」に取り組んでいくうえで、とっても基本的な考え方、「樹形図(じゅけいず)」をかいていきましょう。 百の位には、2、3、4の3通りの並べ方があります。 百の位が2のときの十の位と、一の位を樹形図にかいてみます。 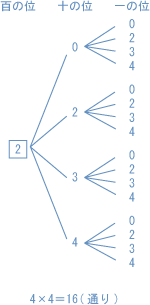 百の位が3、4のときも同じようにかけるので、 16 × 3 = 48(通り) |
| <問題1(2)の考え方と答え> |
| 「4の倍数の特ちょう」は何でしたか? そうですね。「数字の下2けたが、4の倍数か00」であればよかったですね。 (他の倍数の特ちょうも、しっかり復習しておいてね) 0、2、3、4の4種類のカードの組み合わせでつくれる下2けたの4の倍数は、 00 04 20 24 32 40 44 の7通りですね。 では、下2けたが7つ決まったので、樹形図をかきます。 「下2けた」→「百の位」→「千の位」と逆にかきますよ。  千の位は「0」にならないことに注意してね。 それぞれが、 4 × 3 = 12(通り) あるので、全部で、 12 × 7 = 84(通り) |
| 問題2 |
| 1から10までの番号が書かれたカードが1枚(まい)ずつあります。この10枚の中から何枚かを取り出したときに、それらの番号の合計が50になる組み合わせは何通りありますか。 (春日丘中 2007年) |
| <問題2の考え方と答え> |
| これは「逆転の発想」が必要ですね。 50になる選び方、 例えば、1、2、3、4、6、7、8、9、10と書き出していくと、これでも正解は導けますが、時間がかかって、ちょっと大変ですね。 そうじゃなくって、 「どれを選んだら50になるのか?」…と考えないで、 「どれを選ばなければ50になるのか?」…を考えればいいですね。 1から10までをたすと「55」になりますよね。 だから、選んだ数が「50」になるには、合計が「5」になるカードを選ばなければよい、ということになります。 合計が「5」になるカードの組み合わせは? (5) (4、1) (3、2) の3通りだけですね? |
関連するおすすめの記事













![文章の接続語をうまく使うことができません[中学受験]](/_shared/img/ogp.png)
![算数「場合の数」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu23/01.gif)








