算数｢仕事算・ニュートン算｣［中学受験］
■算数「仕事算・ニュートン算」
こんにちは、合格総理大臣 ミスター・ツカムです。
今回もミスター・ツカムと入試問題を考えていきましょう。
今回は「仕事算・ニュートン算」です。実際の中学入試問題を見ても、そんなに難問（なんもん）は出題されていません。基本の考え方をマスターすればだいじょうぶ！
必ずキミのものにできますから、楽しみながらいっしょに取り組んでいきましょう。
| 問題1 |
| Aだけでは28日かかる仕事を、A、B の2人でいっしょにすると12日かかります。この仕事を、B だけですると何日かかりますか。 （日本大学第一中 2008年 第2回） |
| ＜問題1の考え方と答え＞ |
| まずは、仕事算の基本的な問題ですね。 この仕事算のポイントは、「全体の仕事量」を数字で表すことなのです。 1人ができる仕事量を先に決めて、「全体の仕事量」を考えるか？ 「全体の仕事量」を先に決めて考えていくか？ どちらでもいいんです。この問題は2通りの解き方を示してみますね。 ≪解法1≫ 全体の仕事量を先に決める。 「28日かかる」「12日かかる」…とあるので、28と12の最小公倍数を考えます。 28と12の最小公倍数は、84 ですね。  Aはこの仕事を終えるのに28日かかるので、Aが1日にできる仕事量は？  次に、AとBの2人でやると12日かかるので、AとBの2人が1日にできる仕事量は？  B が1日にできる仕事量は？  だから、B だけでこの仕事をすると   28日で仕上げるので、全体の仕事量は？  AとB の2人で1日にできる仕事量を△とすると、問題文から、    だから、B が1人でできる仕事量は？  つまり、B だけでこの仕事をすると、   さて、どちらの考え方がキミにはわかりやすいですか？「ぼくはこっち…」「わたしはこっち…」と決めておくとよいかもしれません。 次に取り上げる問題では、≪解法2≫のように、個人の仕事量を決めますが、もちろん、どちらの解法でも考えられるのがいいですよ。 |
| 問題2 |
| ある仕事をするのに、AさんとBさんの2人で仕事をすると5時間かかります。同じ仕事を、Aさんが1人ではじめてから8時間後にBさんが加わると、Aさんが仕事をはじめてから終わるまでに10時間かかります。AさんとBさんが1時間にできる仕事の量の比を、最も簡単な整数の比で答えなさい。 （市川中 2008年） |
| ＜問題2の考え方と答え＞ |
この問題は線分図をかいて考える基本的な問題です。きっちりマスターしてね。 全体の仕事量は？  また、この仕事を、Aさんが10 時間、B さんが2時間すれば終わります。  いずれも、全体の仕事量を表していて等しいので、  これを線分図にかいてみるとこうなります。 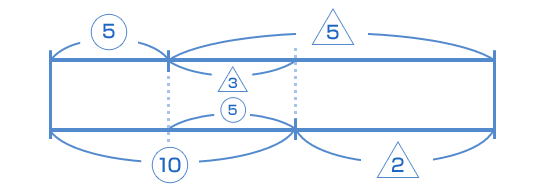  Aさんの1時間の仕事量 × 5 ＝ Bさんの1時間の仕事量 × 3 ですね。 よって、AさんとBさんの1時間でできる仕事量の比は逆比になり、 A ： B ＝ 3 ： 5 です。  |
おすすめのアプリ限定特集
お子さまに関するお悩みを持つ
保護者のかたへ
- がんばっているのに成績が伸びない
- 反抗期の子どもの接し方に悩んでいる
- 自発的に勉強をやってくれない
このようなお悩みを持つ保護者のかたは多いのではないでしょうか？
＼そんな保護者のかたにおすすめなのが／
ベネッセ教育情報サイト公式アプリ
教育情報まなびの手帳
ベネッセ教育情報サイト公式アプリ
教育情報まなびの手帳
お子さまの年齢、地域、時期別に最適な教育情報を配信しています！
そのほかにも、学習タイプ診断や無料動画など、アプリ限定のサービスが満載です。
ぜひ一度チェックしてみてください。
