算数｢相当算・売買損益（1）｣［中学受験］
| 問題5（売買損益） |
| 原価（ア）円のリンゴを（イ）個仕入れました。1個80円で売ると960円の損失で、1個100円で売ると2240円の利益があります。（ア）と（イ）の数字を求めなさい。 （慶應義塾中等部 2007年） |
| ＜問題5の考え方と答え＞ |
| これはおもしろい問題ですね。売買損益と差集め算の合体問題ですね。 ここでも、両方の単元の基本がしっかり定着していると考えがすぐにうかびます。応用問題とは、基本問題の組み合わせなんですね。 原価も個数もわかっていませんが、仕入れた総額をこんな図で表してみました。 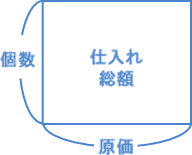 これは面積図ですね。 原価 × 個数 ＝ 仕入れの総額 になっているのが理解できますか？ 個数がわからないけれど、「1個80円で売ると960円の損失」をかいてみます。 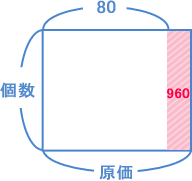 「1個100円で売ると2240円の利益」もかいてみます。こうなります。 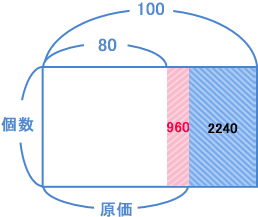 ここまでかくと、もう簡単ですよね？ 960 ＋ 2240 ＝ 3200円 この面積の横の長さは？ 100 − 80 ＝ 20 です。 そして、たての長さ、つまり個数は？ 3200 ÷ 20 ＝ 160 これが仕入れた個数、つまり（イ）です。 「1個80円で売ると960円の損失」の面積図から計算すると、 960 ÷ 160 ＝ 6 原価より6円安く売っていたことになります。 だからリンゴの原価（ア）は、 80 ＋ 6 = 86  |
さて、みなさんいかがでしたか？
この単元をスムーズに理解するには、割合の基本となる小数・分数・歩合（ぶあい）を完ぺきに定着させることが大前提です。この機会に完ぺきにしてくださいね。線分図をかいて解いた問題、○や△の計算だけで解いた問題。いろいろなパターンがあります。これも数多く練習すれば、問題を読んだ瞬間（しゅんかん）に「あ、あのパターンだな。いただき！」ってことになります。
解けたときの喜びはすごいですよ。「ああっ、算数ってすばらしい学問ですねえ」
合格総理大臣 ミスター・ツカム
