中学校数学の統計教育にある四分位範囲とは？　お子さまに質問される前にチェック！

お子さまに「四分位範囲ってなに？」と質問されたら、どうしますか？

2021年度から中学校でも全面実施となる新学習指導要領。数学の統計分野では「資料の活用」が「データの活用」という名称に改められ、もともと高校1年生で学習していた「四分位範囲」や「箱ひげ図」を中学2年生で学習することになりました。

今回は、「四分位範囲（しぶんいはんい）」や「箱ひげ図（はこひげず）」をうまく説明するためのポイントを解説します。

「四分位範囲」とは？　何のために使うもの？

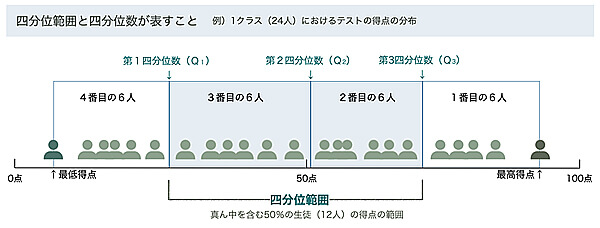
「四分位範囲」とは、データを4等分したときに真ん中を含む50％のデータの散らばりを表したもの。

たとえば、数学の定期テストの得点にどのくらいバラつきがあるのか、お子さまの得点がクラスでどのくらいの位置にあるのかを知るのに便利な考え方です。

四分位範囲を求めるには、データを４分割する「四分位数（しぶんいすう）」という３つの値が必要。低い値から順に「第１四分位数」「第２四分位数」「第３四分位数」と呼びます。

「第３四分位数−第１四分位数」という引き算で、四分位範囲の値（散らばりを表す値）が分かります。

「四分位数」の求め方は「中央値」の計算方法を復習！

それぞれの四分位数は以下の手順で求められます。

＜四分位数の求め方＞

 (1) データ全体の「中央値」（真ん中の値）を求める（＝第２四分位数）
 (2) 中央値より下のデータの中央値を求める（＝第１四分位数）
 (3) 中央値より上のデータの中央値を求める（＝第３四分位数）

中央値は以下のやり方で計算しましょう。

＜四分位数の求め方の例（データの個数が奇数）＞

 (1) データを小さい順に並べる　→　6　7　8　10　11　14　17
 (2) ど真ん中は「10」　→　中央値（第２四分位数）は「10」
 (3) 下半分の中央値は「7」→第１四分位数は「7」
 (4) 上半分の中央値は「14」→第３四分位数は「14」

＜四分位数の求め方の例（データの個数が偶数）＞

 (1) データを小さい順に並べる　→　3　6　7　8　10　11　14　17
 (2) ど真ん中がない
 (3) 真ん中の２つは「8」と「10」　→　中央値（第２四分位数）は（8＋10）÷2＝「9」
 (4) 下半分（3　6　7　8）の中央値は（6＋7）÷2＝6.5 →第１四分位数は「6.5」
 (5) 上半分（10　11　14　17）の中央値は（11＋14）÷2＝12.5→第３四分位数は「12.5」

「箱ひげ図」の書き方は最小値・四分位数・最大値がポイント

四分位数・四分位範囲・最小値・最大値を図にしたのが「箱ひげ図」です。２つの箱が真ん中でくっつき、前後（または上下）にヒゲがついた形をしています。

箱ひげ図が長くなるほどデータの散らばりが大きいことを表します。

作成に必要な５つの値（最小値・第１四分位数・第２四分位数・第３四分位数・最大値）を求めたら、早速書いてみましょう。

＜箱ひげ図の書き方＞

 (1) 最小値・第１四分位数・第２四分位数・第３四分位数・最大値のところに線を引く
 (2) 第１四分位数と第３四分位数を表す線の両端をそれぞれ直線でつなぎ、長方形にする
 (3) 箱の前後（または上下）にヒゲを書く