分数の計算をわかりやすく教えるには？つまずきやすい通分をするたし算・ひき算を解説！【小学校高学年】

小学校の高学年から習う分数の計算は、算数の学習の中でとてもつまずきやすいところです。分数には真分数・仮分数・帯分数といった種類がいくつかあり、さらに通分や約分まで出てくるので、混乱してしまうのです。
今回は、分数の計算の基本である真分数のたし算・ひき算について解説します。

分母が異なる分数は、分母をそろえる

分数のたし算やひき算は分母が異なっているとたし算・ひき算ができません。よくある間違いは、分母がそろっていないのに分母どうし・分子どうしでたしたりひいたりしてしまうことです。

なぜそれがいけないのかがわからないので、そのような間違いをしてしまうのです。まずは、分数の意味から考えてみましょう。

分母が異なると数の大きさが違うことを意識させる

そもそも分数とは「１つのものを同じ大きさに分けたものがいくつ分あるか」を表します。いくつに分けたかによって、分けたものの１つあたりの大きさは変わります。そのいくつに分けたかを表すのが分母の数です。

同じ分母であれば、１つあたりの大きさは同じです。例えば「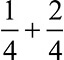」の計算の意味は、「４つに分けたものの1つ分と４つに分けたものの２つ分を合わせるとどうなるか？」です。合わせると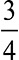で、４つに分けたものの３つ分になりますね。分母が同じであれば、分子の数をたせばよいのです。

しかし、分母が違うと１つ１つの大きさが違うので、単純にたすことはできません。また、分母どうしをたしてしまうと、分け方も変わるのでおかしくなります。

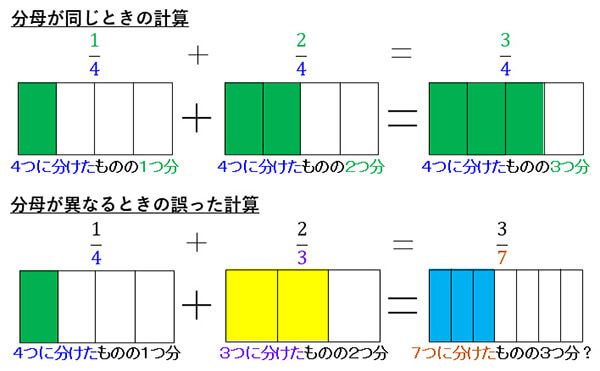
まずは、同じ大きさに分けたものどうし、つまり、分母が同じでないと計算できないということを意識させることが大事です。

分母と分子に同じ数をかけても大きさは変わらない

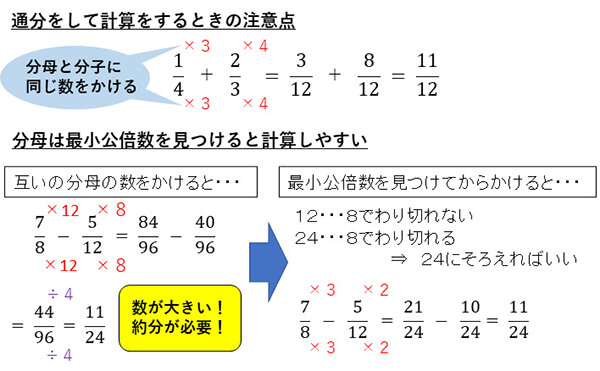
分母がそろっていないときは分母をそろえるのが「通分」です。通分をするのに用いる考え方は、分母と分子に同じ数をかけても大きさは変わらないということです。

例えば、分母に２をかけると、分ける数が２倍になります。その分、１つ分の大きさが半分になるので、分子のほうも２倍すればもとの大きさになります。これは、３倍でも４倍でも同じです。

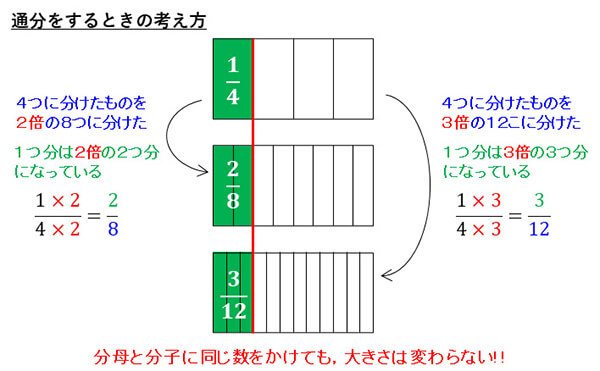
分母と分子に違う数をかけてしまうと大きさが変わってしまいます。分母と分子には必ず同じ数をかけるということを覚えさせましょう。

通分をするときの最小公倍数につまずいてしまったら？

通分をするときにどのような数をかければいいのか、ここでつまずく子も多いです。一言で言えば「２つの数の最小公倍数にする」ですが、それが理解しにくい部分でもあります。

では、「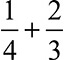」の計算を考えましょう。
分母が４と３でそろっていないので、そろえるために通分をします。４と３の最小公倍数、すなわち、４の倍数と３の倍数の共通な数でいちばん小さいものはいくつか？を考えます。

最小公倍数の見つけ方は、分母が大きい数の倍数を考えていき、それが小さい数の分母の倍数になっているかを考えます。「小さい方の分母でわり切れるか」と考えるのがわかりやすいですね。ここでは大きい方の分母は４になるので、４の倍数を考えていきます。
　４・・・３でわり切れない　⇒　公倍数でない
　８・・・３でわり切れない　⇒　公倍数でない
　１２・・・３でわり切れる　⇒　公倍数　⇒　いちばん小さいので最小公倍数
よって、分母を１２にそろえればよいとわかります。
４×３＝１２なので、の分母と分子に３をかけて、３×４＝１２なので、の分母と分子に４をかけます。分母がそろったら、分子どうしをたせばいいです。このとき、分子に分母と同じ数をかけ忘れたり、分母どうしをたしてしまったりすることに注意しましょう。

分母のそろえかたとして、「互いの分母の数をそれぞれかける」という方法もあります。次の例では、それぞれ３と４をかけています。この方法でもよいのですが、数が大きくなってしまうことと、約分をする必要が出てきてしまいます。最小公倍数を見つけてからかけると、約分をすることもありますが、数も小さくて計算しやすいので、こちらの方法をしっかりと覚えておくとよいでしょう。