わかるようでわからない…いまさら聞けない「偏差値」とは？

わかるようでわからない偏差値の疑問を解説！

偏差値とは、ある集団の中での位置を示す数値のこと。
平均点をとった人の偏差値を50として平均点より得点が上なら偏差値は51、52…となり、得点が平均点以下ならば49、48…となる。
成績を見るときは、得点、順位などを確認するが、例えば国語が60点、英語が50点だった場合、国語の方がよい成績とはいえない。なぜなら得点は国語と英語の問題の難易度も影響するからだ。

しかし、偏差値では受験した集団の中での自分の客観的な学力位置がわかる。例えば、国語の偏差値が55、英語が50だったら国語の方がよい成績だと言える。

具体的に解説しよう。
【例】Aさんの偏差値（得点60点　平均点50点の時）
(1) 標準偏差20
(2) 標準偏差10　の場合

(1) （60－50）÷20×10＋50＝55　　←Aさんの偏差値は55になります
(2) （60－50）÷10×10＋50＝60　　←Aさんの偏差値は60になります

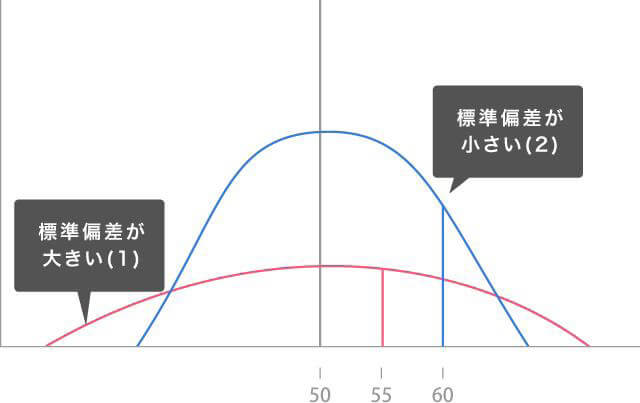
偏差値が50より大きい場合には、同じ得点・平均点であっても、標準偏差（得点の散らばり）が大きいほど偏差値は低くなる。また、平均点ならば標準偏差（得点の散らばり）に関わらず偏差値は50となる。

偏差値を正しく使って「学力」の伸びを確認していこう！

偏差値を見る際に注意したいのは、偏差値は母集団が異なれば比較できないということ。
例えば、同じ高校内や、受験する層や人数がある程度一定の模試であれば、偏差値を指標に各回の模試で学力を比較することができるが、中学校の偏差値と高校の偏差値や、模試受験者の人数やレベルが異なる模試同士の比較は意味がない。

高校の教室や進路室に大学の難易度一覧のポスターが貼ってある場合も、そのポスターに掲載されている偏差値はあくまでその模試会社が実施した模試の偏差値。違う模試の偏差値で難易度を比較することはできないのだ。
それらの前提を押さえたうえで、偏差値を今後の学力の伸びの指標として有効に使っていこう。

文／進研ゼミ高校講座　受験情報担当　高山