算数「年齢算・仕事算」[中学受験]
お気に入りに登録
■算数「年齢算・仕事算」
こんにちは。合格総理大臣 ミスター・ツカムです。
「急がば回れ」ということわざがあるように、算数の上達には基礎(きそ)をしっかり定着させること。これが重要ですよ。
今回は特殊(とくしゅ)算の中から、年齢(ねんれい)算と仕事算を取り上げます。線分図をしっかりかけるように練習してくださいね。
では、さっそく問題をみていきましょう。
| 問題1(年齢算) |
| 現在、父の年齢(ねんれい)は36才で、子どもの年齢の4倍にあたります。 父の年齢が子どもの年齢の2倍になるのは 年後です。 (名古屋女子大学中 2007年・特別奨学生) |
| <問題1の考え方と答え> |
| この年齢算の問題は、6年生の後半になっても力づくで解こうとする人がいます。 父: 36 37 38 39 40 41 … 子: 9 10 11 12 13 14 … ??? 「まだだなあ」 って(笑) この機会に線分図で解くことを覚えてね。 この問題もそうですが、 父は現在36才で、子どもの4倍とありますから、子どもは9才ですね。 それが数年後に2倍になるので、線分図はこうなります。 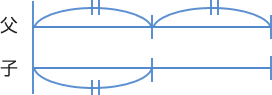 次に、父36才、子ども9才をかきます。ここがミソ! 次のようにかきます。 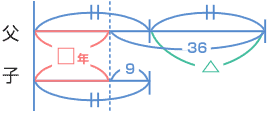 図の赤の線の部分が 年たった…ことを表しています。 線分図をよく見ると、△の部分が何才分か?…わかりますね。 36 − 9 = 27 です。 そうです。この「ひと山」が27だから、2倍は54才(父)ですね。子どもが27才。 ちょうど2倍になります。 何年後と聞かれていますので、 54 − 36 = 18 です。 |
| 問題2(年齢算) |
| 現在、子ども3人の年れいの和と父の年れいの比は4:7で、9年後には子ども3人の年れいの和と父の年れいは等しくなります。現在の父の年れいは 才です。 (関東学院中 2007年) |
| <問題2の考え方と答え> |
まず、子ども3人の年齢の和と父の年齢の比が、4:7 という線分図をかきます。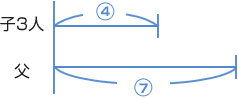 9年後に、子ども3人の年齢の和と父の年齢は等しくなります。 子どもは3人なので、 9 × 3 = 27 増えます。 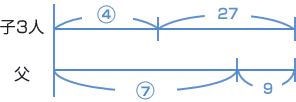 線分図をよく見ていると、 27−9=18(才)が○いくつ分になっているのかがわかりますね? 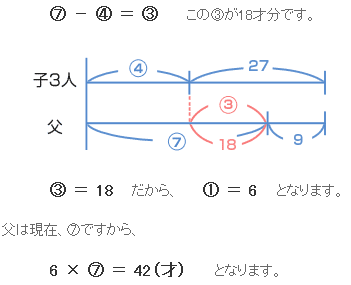 |
関連するおすすめの記事













![算数「年齢算・仕事算」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu10/01.gif)
![算数「仕事算・ニュートン算」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu21/01.gif)








