算数の文章題が苦手です[中学受験合格言コラム]
お気に入りに登録
「算数の文章題が苦手です」
平山入試研究所の小泉浩明さんが、中学受験・志望校合格を目指す親子にアドバイスする実践的なコーナーです。保護者のかたから寄せられた疑問に小泉さんが回答します。※小泉さんへのご質問は、不定期にBenesse教育情報サイトメンバー向けのメールマガジン「教育発見隊通信」で募集をいたします(随時の受付は行っておりません)。

質問者
相談者:小6女子のお母様質問
算数の文章題が苦手です。読解力の問題なのでよく本を読みなさい、と言われますが本を読むのは好きなのです。割り算をすればよいのか、それとも掛け算か?というので混乱するようで、小数点や分数が入るともうパニックです。小泉先生のアドバイス
本を読んで理解する力と、算数の文章題を読んで理解する力は必ずしも一致しない
「本を読むのは好き」ということですが、本を読んで理解する力と、算数の文章題を読んで理解する力(さらに解く力)は必ずしも一致しないと思います。なぜなら、算数の文章題には特有の≪約束ごと≫があるからです。
たとえば次のような問題を考えてみましょう。簡単な仕事に関する問題です。
仕事に関する問題を解くには、いくつかの方法があります。たとえば全体の仕事量を1とし、A君とB君の1日の仕事量を計算します。そしてそれらを足すことで、2人でいっしょにした場合の1日の仕事量を計算します。図で説明すると、以下のようになります。
さて、ここでの≪約束ごと≫とは、このような仕事に関する問題を解くには、「1日の仕事量」を考える必要があるということです。そしてこのような≪約束ごと≫は教えてもらって十分に理解しなければ、なかなか使えるようにはなりません。さらに十分に理解するためには、計算式だけではなく、上記のような「図」を使うことで、何をやっているのかを具体的に実感することが大切です。そういったプロセスがないと、数値が少し複雑になっただけでわからなくなります。
たとえば、次のような問題はどうでしょうか。
この問題では、A君の仕事量の図がかきにくいですが、考え方は同じです。
算数の文章題を解くためには、≪約束ごと≫つまり問題に対する考え方を学ぶ必要があり、本を読む力とは別物であることを説明してきましたが、おそらくお子さまに今一番大切なことは、数式を図と結び付けて勉強することだと思います。それにより「自分は何をやっているのか?」を常に意識することができるようになるでしょう。問題演習を重ねることで、数式だけでも考えられるようになりますから、最初のうちはぜひ図を活用してみてください。
「本を読むのは好き」ということですが、本を読んで理解する力と、算数の文章題を読んで理解する力(さらに解く力)は必ずしも一致しないと思います。なぜなら、算数の文章題には特有の≪約束ごと≫があるからです。
たとえば次のような問題を考えてみましょう。簡単な仕事に関する問題です。
| A君1人だと3日、B君1人だと6日かかる仕事を2人でいっしょにすると、何日で終わりますか。 |
仕事に関する問題を解くには、いくつかの方法があります。たとえば全体の仕事量を1とし、A君とB君の1日の仕事量を計算します。そしてそれらを足すことで、2人でいっしょにした場合の1日の仕事量を計算します。図で説明すると、以下のようになります。
| 〔解答例〕 全体の仕事量を1とする。(図1) A君は3日かかるから、1日の仕事量は、 1÷3=1/3(図2) B君は6日かかるから、1日の仕事量は、 1÷6=1/6(図3) A君とB君がいっしょにする場合の1日の 仕事量は、 1/3+1/6=1/2(図4) ですから、仕事が終わるまでの日数は (全体の仕事量は1であるから!)、 1÷1/2=2(日) | 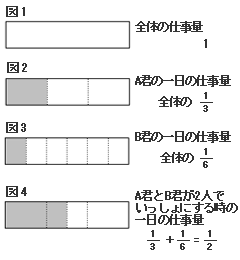 |
さて、ここでの≪約束ごと≫とは、このような仕事に関する問題を解くには、「1日の仕事量」を考える必要があるということです。そしてこのような≪約束ごと≫は教えてもらって十分に理解しなければ、なかなか使えるようにはなりません。さらに十分に理解するためには、計算式だけではなく、上記のような「図」を使うことで、何をやっているのかを具体的に実感することが大切です。そういったプロセスがないと、数値が少し複雑になっただけでわからなくなります。
たとえば、次のような問題はどうでしょうか。
| A君1人だと0.4日、B君1人だと2日かかる仕事を2人でいっしょにすると、何日で終わりますか。 |
この問題では、A君の仕事量の図がかきにくいですが、考え方は同じです。
〔解答例〕
全体の仕事量を1とする。
A君は0.4日かかるから、1日の仕事量は、
1÷0.4=10/4
B君は2日かかるから、1日の仕事量は、
1÷2=1/2
A君とB君がいっしょにする場合の1日の仕事量は、
10/4+1/2=10/4+2/4=12/4=3
ですから、仕事が終わるまでの日数は、
1÷3=1/3(日)
全体の仕事量を1とする。
A君は0.4日かかるから、1日の仕事量は、
1÷0.4=10/4
B君は2日かかるから、1日の仕事量は、
1÷2=1/2
A君とB君がいっしょにする場合の1日の仕事量は、
10/4+1/2=10/4+2/4=12/4=3
ですから、仕事が終わるまでの日数は、
1÷3=1/3(日)
算数の文章題を解くためには、≪約束ごと≫つまり問題に対する考え方を学ぶ必要があり、本を読む力とは別物であることを説明してきましたが、おそらくお子さまに今一番大切なことは、数式を図と結び付けて勉強することだと思います。それにより「自分は何をやっているのか?」を常に意識することができるようになるでしょう。問題演習を重ねることで、数式だけでも考えられるようになりますから、最初のうちはぜひ図を活用してみてください。
みんなが読んでる!おすすめ記事
- デマ拡散や著作権侵害、起きやすい子どものスマホトラブル注意点【メディアリテラシー編】
- 「○○さんと同じクラスにしてほしい」と先生に頼むのは、わがままでしょうか?[教えて!親野先生]
- 【回答:日高のり子・森上教育研究所】志望校選び<その8>
- 私立批判はタブー?[中学受験合格言コラム]
- 進路が決まらない!そんな時に、高校生と保護者がやるべきこと【体験談あり】
- 【回答:日高のり子・森上教育研究所】志望校選び<その6>
- 大学への「社会的要請」とは? 学術会議、国立大の再編に批判
- クラス替え 仲のよい友達とクラスが分かれて元気がない我が子…何と声をかける?
- 【回答:日高のり子・森上教育研究所】志望校選び<その3>














![「○○さんと同じクラスにしてほしい」と先生に頼むのは、わがままでしょうか?[教えて!親野先生]](/img_o/kj/kyouiku/201003/20100309-1.jpg)










