謎解きから、筋道を立てて考える力を養う算数の授業［こんな先生に教えてほしい］

毎週のように学校を訪ね、たくさんの授業を見ています。そして、先生方から授業への想いを聞いています。
小学生から高校生、そして、先生や保護者のかたに役立つ教育番組を制作するためです。その中で、「こんな先生に教えてほしい」と思った先生方のことを書かせていただきます。

今回紹介するのは、熊本県のAP先生です。授業は、小学6年生の算数です。
問題は「9人一人ひとりが全員にパスを出すとパスの回数は、全部で何回か？ただし、同じ相手にパスを出せるのは1回だけ」。


子どもたちの目標は、わかったことを言葉にすることです。ちなみに、みんなはそれを「言葉の式」と呼んでいます。そして、AP先生が目指すのは、常に算数を通じて筋道を立てて考える力を育てることです。なぜなら、わかる楽しさを知る第一歩と考えているからです。

授業は、先生が授業のタイトル「直線で結ぼう」を張り出すことから始まりました。そして、問いかけます。点と点を結ぶ、直線の数は？

まずは、点が1つの時は、直線は何本引ける？　　0本です。
では、点が2つの時は、直線は何本引ける？　　　1本です。
そして、点が3つの時は、直線は何本引ける？　　答えが2本派と3本派に分かれました。
まず3本派は、次のように考えました。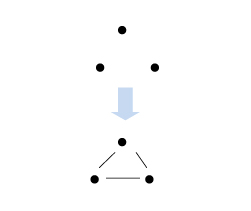


一方、2本派、は次のように考えました。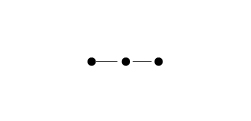


どちらも正しい。そこで、先生は、ルールを決めます。「1つの点から別の点には、必ず直線が引けることにする」。つまり今回は……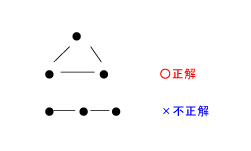


としました。

では、点が4つの時は、直線は何本引ける？

ここから、先生はひとつだけ指示を出します。「頭の中で考えて！」そして、みんながイメージできるよう3分時間を取りました。答えは、周りを囲む4本の線と対角線2本で、計6本です。
　
では、点が5つの時は、直線は何本引ける？　頭の中でイメージしてください。

間髪をいれず、点が6つの時は、直線は何本引ける？と畳み掛けます。
さらに、点が7つの時は？　点が8つ、点が9つだったら直線は何本引ける？と続けていきます。そして、先生は「頭の中でイメージして！ 書かないように！」と言い続けます。これは、「線を引きたい！」という意欲を高めることを狙っています。「ちょっと抑制を加える」これも教えるテクニックの1つです。

頃合いを見て、先生は、「じゃ各自好きに考えてみよう！」と促します。多くの子どもたちは、図を書き調べ始めました。中に、表を使い規則性から調べようとしたり、式を考えたりする子どももいます。ちなみに、このクラスでは、図を書く人は20人。表を書く人は8人。式（計算）は6人でした。

10分位たつと、図からアプローチしている子どもたちの手が止まりはじめました。線が多くてうまく数えられないのです。「うまくいかない！」ことを十分体感したところで、先生は、線を引きやすいよう9つの点を印刷したプリントも手渡します。そして、「数えやすくするにはどうしたらいい？」と投げかけます。

子どもたちからは……

●一個の点から順番に行く
●周りから引き始める
●色分けしながら引く

などの、数えやすい直線の引き方のモデルが出されました。きれいに線を引けるようになると、1つの点から8本の線が引けることに気付いた子どもの中から、
8＋7＋6＋5＋4＋3＋2＋1＝36
という考え方が出されました。

一方、まだどうしてよいかわからない子どもたちに対して、先生は、一緒に考えるヒントコーナーを開きます。これは、用意した稼働式のホワイトボードの陰で開かれる、先生による個人授業です。先生とのヒソヒソ話で、自分だけがわかったことがある。その優越感がやる気を高め、学習意欲の持続につながります。
ここでは、先生は「線を引いて数えるのは、難しい」という子どもたちの意見を聞いて、表を使い、きまりを見つけることにしました。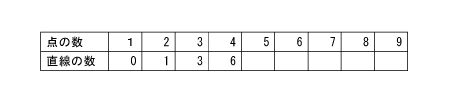

きまりを見つけるには、縦と横で見る方法があることを確かめたあと、まず横から見てみます。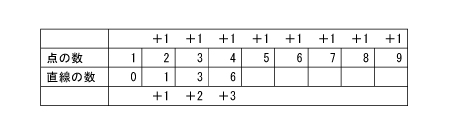
点が、「＋1」ずつ増えるのに対して、直線は、＋1、＋2、＋3となります。これを見た子どもたちは、ダッシュで自分たちの机に戻っていきます。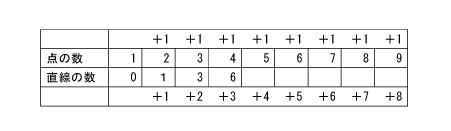

中には、表を縦に見てきまりを考える子どももいます。
たとえば……求めたい点の数の前の点の数＋直線の数＝次の直線の数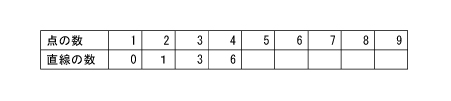

つまり、「求めたい点の数が2としたら、直線の数は1＋0＝1、言い変えると……　点の数＋直線の数＝次の直線の数」。

ほかにもこんな言葉の式にした子どももいます。
言葉の式「点の数×ひとつの点で結べる直線?ひとつの点で結べる数の以下すべての和」、これは、「求めたい点の数が9としたら、9×8−36ということです。36は、8以下の和、8＋7＋6＋5＋4＋3＋2＋1」です。
そんななか……「『点の数×ひとつの点で結べる直線』を2で割る」、つまり、「9×8÷2＝36」という言葉の式が出されました。

ここで面白いのが、なぜ「÷2」なのかと聞いても、子どもたちは「うまく説明ができない」と言うのです。「図を書いて、8＋7＋6＋5＋4＋3＋2＋1を思いつき、表を見て答えがあらかじめわかったうえで、式にしようとしていて、これまでわかったことを整理し結びつけようとした時思い浮かんだ」そうです。

ちなみに、この「9×8÷2＝36」は、AP先生が目指した答えのひとつです。「÷2」は重複した線を除くためなのですが、正直なところ、「よく思いついたな……！」というのが感想です。このあと、子どもたちは、みんなで謎解きに夢中になっていきました。

AP先生の授業のモットーは、子どもたちから、「今日の問題は難しかったけれど楽しかった」「今まで嫌いだった算数が少し好きになりました」と言われることだそうです。

まさに、そのとおりの授業でした。