公式丸暗記では応用問題に歯が立たない!? 解決策を中学受験の専門家がアドバイス
中学受験の算数で、公式を暗記はしているが応用問題が解けない、と悩む保護者は多いのではないだろうか。「公式を使いこなせるようになるには、意味もわからず暗記するだけではだめ。試験場で公式を忘れてもいいように、自分で導けるようになるまでの深い理解が必要です」と話すのは、平山入試研究所の小泉浩明氏。具体例を挙げてアドバイスをもらった。
＊＊＊
【質問】
算数で公式の意味を理解せずに丸暗記し、そのまま解こうとするので、ひねった応用問題を解くことができません。（小6女子の母親）
【小泉氏からのアドバイス】
対応できない理由としては、公式自体を忘れるということが考えられます。たとえば「速さの公式」には次の3つがあり、その公式を覚えるのに便利な図が「はじきの図」です。
〔速さの公式〕
（速さ）×（時間）=（距離）
（距離）÷（速さ）=（距離）
（距離）÷（時間）=（速さ）
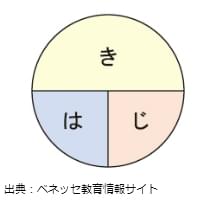
図にある「き」は「距離」、「は」は「速さ」、「じ」は「時間」を表します。この図が便利なのは、たとえば「速さ」を求めたい時は、「は」の部分を隠すと、「き／じ（上下関係＝わり算）」となり、「（距離）÷（時間）」にすればよいことがわかります。同様に「距離」を求めたい時は「き」を隠し、「時間」を求めたい時には「じ」を隠すと公式が導けます。
もう少し原理・原則に基づいた覚え方、あるいは理解のしかたは、「距離」を「速さ」と「時間」をかけ合わせて得られる「面積」と考える方法です。
この覚え方のすばらしさは、「距離は面積」ということを忘れなければ、四角形の面積を求めるように、縦（速さ）×横（時間）＝（距離）という関係を自分で導けるようになることです。そして、四角形を思い浮かべることで、残りの2つの式も導けます。このように、公式を忘れても大丈夫なように、「自分で導けるようにしておく」ことを学習の目標としておくとよいでしょう。
