算数「数の性質」[中学受験]
お気に入りに登録
■算数「数の性質」
こんにちは。合格総理大臣 ミスター・ツカムです。
今回は「数の性質」を取り上げますよ。この単元は倍数、約数、素数(※)…などの整数の性質をしっかり理解することが重要です。
パズル的な問題で、推理(すいり)やひらめきが必要なこともあります。慣れていない人は最初はなじめないかもしれませんが、しっかり基礎(きそ)を定着させてください。
何度も言いますが、応用問題は基本問題の組み合わせです。
では、さっそく始めていきましょう。
(※)素数 : 2、3、5、7のように、1とその数以外に約数をもたない自然数のことを「素数」といいます。
| 問題1 |
| 100の約数は何個ありますか。 (多くの中学入試で出題される一般的な問題です) |
| 問題1の考え方と答え |
| このような問題は、力ずくで答えを見つける人もいるでしょうね。 100ぐらいの数だと可能ですね。 1、2、4、5、10、20、25、50、100 …で、9つです。 でももし、500とかだったら少し大変です。5000とかもやりますか?(笑) この機会に、簡単(かんたん)に約数の数を見つける方法を身につけましょう。 整数(自然数)を「素数だけのかけ算」で表すと、とっても簡単に見つかるんですよ。 100ならこんなふうに見つけますね。 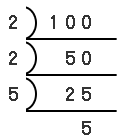 100 = 2 × 2 × 5 × 5 と、かけ算の形で表せます。 この素数のかけ算の組み合わせによって約数が見つけられます。 2 × 2 = 4 2 × 5 = 10 2 × 5 × 5 = 50 …のように。 つまり、素数の「2」と「5」を、それぞれ何回使ったかの組み合わせの数が、約数の個数です。 表をかいてみます。 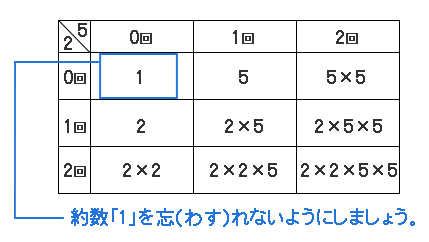 「2」を0回、1回、2回の3通り、 「5」を0回、1回、2回の3通り使った組み合わせの数で、 3 × 3 = 9 約数は9個です。 上の問題ができたら、1000の約数の数を求めてみてください。 |
| 問題2 |
| 4けたの整数があります、その数を9倍すると、数字の並(なら)び方の順序がもとの整数と逆の4けたの整数になりました。もとの4けたの整数は です。 (大阪星光学院中 2008年) |
| <問題2の考え方と答え> | ||
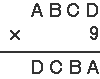
| この問題はパズル的な問題ですね。ひらめく人は一瞬(いっしゅん)で解けてしまいますね。 まず、アルファベットを使って筆算を書いてみます。
ここでまず、Aについて考えると、Aが2以上ならこの式は成立しませんよね。 A × 9 は2けたになりますから、かけ算すると5けたになってしまいます。 だから、A = 1 で決まりです。 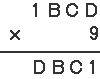 次に、一の位の計算を考えます。D × 9 で、一の位が「1」になるかけ算は、9 × 9 = 81しかないです。 だから、D = 9 で決まりですね。 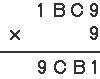 次に、百の位の計算を見ると、B × 9 で、Bが2以上の数だとくり上がってしまい、5けたになってしまいますから、この式は成立しません。 だから、B = 0 か、B = 1 のどちらかです。仮にB=0 としてみます。 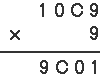 9 × 9 = 81 で「8」がくり上がりました。十の位を「0」にするには「2」が必要なので、 9 × C の一の位が2になるときを考えると、 9 × 8 = 72 これならOKです。つまり、C=8です。 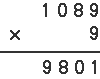 こんなふうに、どの位の計算に目をつければよいか、推理(すいり)して解いていく問題は楽しいですね。慣れない人は何度も同じような問題をさがして練習しましょうね。 |
関連するおすすめの記事













![算数「数の性質」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu13/01.gif)








