理科「てことてんびん」［中学受験］
| 問題3 |
| 「ばね」と「てこ」について、次のような実験を行った。以下の問いに答えよ。ただし、用いたばねはすべて同じものである。 ＜実験1＞ 図1のように、ばねにおもりをつるし、おもりの重さと、ばねの長さとの関係を調べた。その結果は、グラフのようになった。 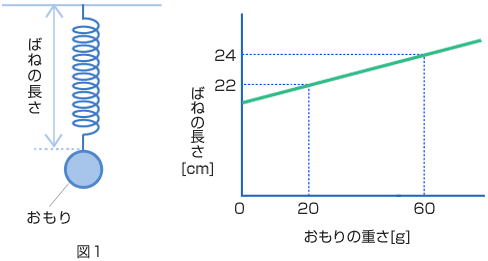 問1 おもりをつるさないとき、ばねの長さは何cmか。 次に、長さ110cm、重さ50gで太さが一様な棒P、Qと重さ10gのおもり8個を用意する。 ＜実験2＞ 図2のように、棒Pの中心から左へ33cmのところにばねをつけ、その反対側を地面に固定した。棒Pの右端（はし）には棒Qとおもり1個をつるす。棒Pの中心を糸で引き上げたとき、地面から、ある高さのところで棒Pは水平になって、つりあった。 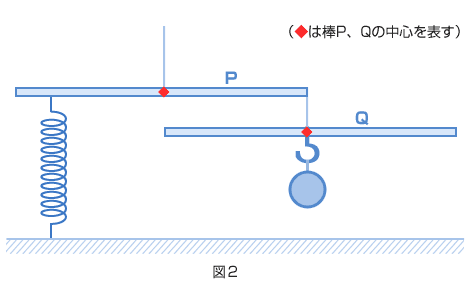 問2 棒Pの地面からの高さは何cmか。 ＜実験3＞ 図3のように、棒Qの中心から左へ5cmの点Rに糸を結び、その糸を棒Pの中心から右に10cmのところに結ぶ。棒Pの左端にフックAをつけ、棒QのRから左に15cmのところにフックB、右に35cmのところより遠くにフックCをつける。おもり8個すべてをフックA、B、Cにつるし、棒Pの中心をばねでつるすと、棒P、Qはいずれも水平になってつりあった。 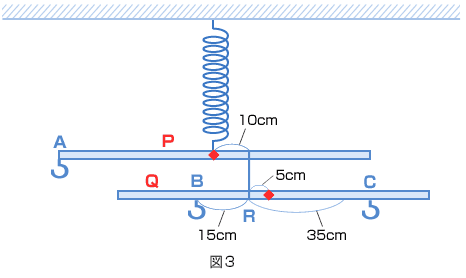 問3 このとき、ばねの長さは何cmか。 問4 フックAにつるすおもりは何個か。 問5 フックBにつるすおもりは何個か。 問6 フックCの位置は棒Qの右端から何cmのところか。 （早稲田中 2008年 第1回） |
| ＜問題3 問1の考え方と答え＞ |
| グラフより、おもりの重さが40g増えるとばねの長さは2cmのびるので、 → 1cm のびるには 20g 必要とわかる。 だから、おもりをつるさないときのばねの長さは、 22 − 1 ＝ 21  |
| ＜問題3 問2の考え方と答え＞ |
| 棒（ぼう）Pの高さというのは、ばねののびたときの長さと同じですね。 だからばねの長さを求めればいいのです。 棒Qとおもりを一つのものとしてわかりやすく図にすると次のようになります。 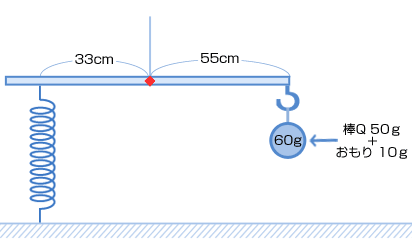 これがつりあっているので、 ばねにかかる力の大きさを□gとすると、 □ × 33 ＝ 60 × 55 □ ＝ 100（g） ばねに100g の力がかかっています。 問1から、ばねののびは？ 100 ÷ 20 ＝ 5（cm） のびています。 だから、 ばね全体の長さは？ 21＋5＝26（cm）  |
| ＜問題3 問3の考え方と答え＞ |
| ばねを下向きに引く力は、棒2本の重さとおもり8個の重さの合計です。 おもりがどの位置にあっても関係ないから、全体の重さは？ 50 × 2 ＋ 10 × 8 ＝ 180（g） ばねののびは？ 180 ÷ 20 ＝ 9（cm） ばねの全体の長さは？ 21 ＋ 9 ＝ 30（cm）  |
| ＜問題3 問4の考え方と答え＞ |
棒Pを一つのものとして整理して図をかきます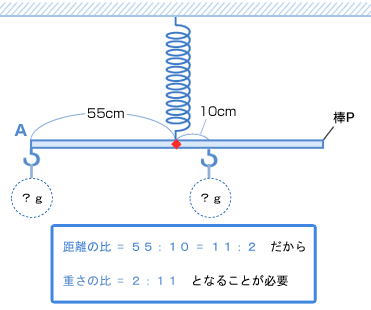 支点からの距離（きょり）は、55cm と 10cm だから、距離の比は 55 ： 10 ＝ 11 ： 2 つりあうためには重さは逆比になり、 2：11 になることが必要です。 重さは、おもり8個（80g）と棒Q（50g）で、130g。   |
| ＜問題3 問5の考え方と答え＞ |
| 問4でAにおもりを2個つけることがわかりましたので、残りは6個。 ここで問題なのは、Cの位置が「35cm より長い」…という条件です。正確な数値が出ていないので、力のつりあいの計算では求められません。BとCにつるす数をあてはめて考えていくしかありません。 支点からの距離を見れば、Bのほうがおもりを多くつるすことはわかりますよね。 右側の力は、棒Qの重さとCにつるすおもりの重さ。 適当に予想をつけて考えていきます。 （Bの数，Cの数）＝（5，1）、または（4，2）、または（3，3）と予想をつけます。 最初の（5，1）をためしてみましょう。 左側にかたむけるはたらきの大きさは？ 50 × 15 ＝750 ですね。 右側にかたむけるはたらきの大きさは？ 棒Qの重さ × 支点からの距離 ＋ Cにかけるおもりの重さ × 支点からの距離 だから、支点RとCとの距離を□cmとすると、 50 × 5 ＋ 10 × □ 左右がつりあっているので、 750 ＝ 250 ＋ 10 × □ □＝ 50（cm） となり、うまくいきました。（←最初のトライでラッキー！） 不安な人は（4，2）でも計算してみてね。 これだとうまくいかないから（5，1）で正しいとわかるよ。  |
| ＜問題3 問6の考え方と答え＞ |
| Rから右端（はし）まで60cm あるので、 60 − 50 ＝ 10（cm）  どうですか？ むずかしいようで基本的な問題の組み合わせでしょ？ わかりやすいように、自分で図をかくと考えが整理できていいですよ。 では、次はちょっとおもしろい問題です。 |
