理科「てことてんびん」［中学受験］
| 問題4 |
問1 図1のような600gの直方体おもりがあります。この直方体おもりを、図2のように軽い板と300gのおもりを使ってつりあわせました。直方体おもりの底面の中心は支点から何cmの位置になりますか。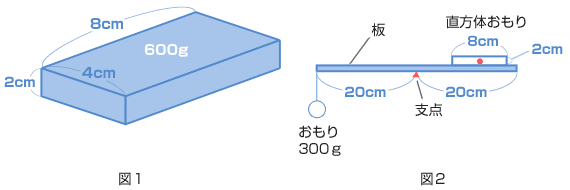 問2 図3のように、直方体おもりを、板のはしにあわせて立てて、つりあわせました。左はしにつるしたおもりの重さは何gですか。 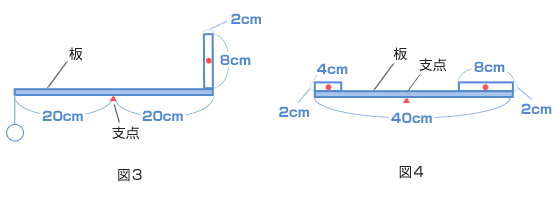 問3 図1と同じ直方体おもり2つを、図4のようにそれぞれ板の両はしにあわせ、つりあわせました。このときの支点は板の左はしから何cmの位置になりますか。 問4 図5のような重さ1.2kgの本があります。図6のように、本を机のはしから18cmはみ出して置き、直方体おもりを本の左はしにあわせてのせました。直方体おもりを右に動かしていくと、やがて本は机から落ちてしまいます。本を落とさずに、直方体おもりを右へ何cmまで動かすことができますか。 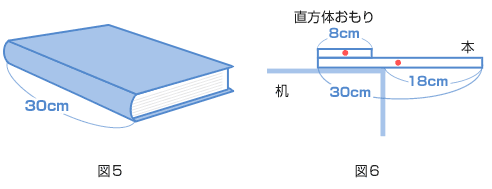 問5 机のはしに同じ2冊の本を重ねて置きました。図7のように、下の本が机のはしから20cmはみ出しても落ちないようにするには、上の本はどこに置けばよいですか。上下の本のずれの範囲（はんい）で答えなさい。ただし、上の本は机にふれてはいけないものとします。 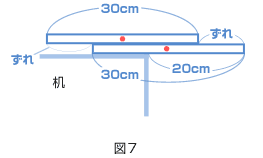 （桐朋中 2005年） |
| ＜問題4 問1の考え方と答え＞ |
| さて、このような立体のものでも、重さは重心一点にかかっていると考えます。では、この直方体おもりの重心はどこ？ 底面積の中心ですね。長方形の対角線を結んで交わったところです。 重心の位置を支点から□cm とすると、 300 × 20 ＝ 600 × □ が成り立ちますね。 □ ＝ 10（cm）  |
| ＜問題4 問2の考え方と答え＞ |
| 直方体おもりの重心の位置は、支点から 20 − 1 ＝ 19cm になりますね。 おもりの重さを□gとすると、 □ × 20 ＝ 600 × 19 □ ＝ 570（g）  |
| ＜問題4 問3の考え方と答え＞ |
| 両方の重心から重心までの距離（きょり）は、 40 − 2 − 4 ＝ 34（cm） です。 重さは同じ600g だから、ちょうど中央に支点がくればいいので、 34 ÷ 2 ＝ 17 左はしから 2＋17＝19（cm）  |
| ＜問題4 問4の考え方と答え＞ |
18cmずらしたので本の重心は机（つくえ）からはみ出してしまいました。このままでは本は落ちてしまいますね。整理して図にしてみましょう。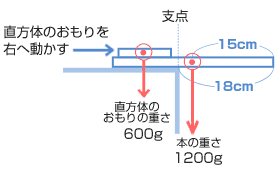 直方体おもりを右に動かして、ぎりぎりつりあうところは？ 支点から直方体おもりの重心までの距離を□cmとすると、 600 × □ ＝ 1200 × 3 □ ＝ 6（cm） 支点から 6cm のところがぎりぎりです。 いま、おもりの重心は支点から 8cm のところにありますから、 8 − 6 ＝ 2（cm）  |
| ＜問題4 問5の考え方と答え＞ |
| いま、下の本の重心は机から5cm はみ出しています。 それを支えるためには、上の本の重心は支点から左に5cmのところでつりあいます。 これ以上、右に動かせば本は落ちてしまいます。 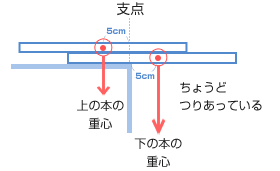 そのときの2冊の本のずれは？ 20 −（5 ＋ 5）＝ 10（cm） では、上の本は左にはどこまで動かせるのでしょうか？ 下の本の左はしぎりぎりまでですね。 上の本の重心が、下の本の左はしにくるときです。 本のずれは？ → 15cm  いかがです？ おもりのかわりが、本になろうがバットになろうが、どんなものでも「重心」の位置さえしっかりおさえておけばだいじょうぶ。自信がついたでしょ？ |
