理科「てことてんびん」[中学受験]
お気に入りに登録
中学受験カウンセラーのミスター・ツカム氏といっしょに、今回も得意単元をふやしていきましょう。
■理科「てことてんびん」
こんにちは。ミスター・ツカムです。今回は理科の「てことてんびん」を取り上げます。この単元では「てこ」「てんびん」「ばね」「輪じく」「かっ車」などの問題が出題されていますね。少し苦手な人もいるかな?
でも安心してください。一度理解できたら問題を解くのが楽しくなるよ。
問題の考え方を簡単(かんたん)に説明すると、てこ とか てんびんの「支点」を見つけて、「左にかたむけるはたらき」と「右にかたむけるはたらき」がつりあっている、ということや、
「上に持ち上げるはたらき(上向きの力)」と「下に落ちようとするはたらき(下向きの力)」が
つりあっている…ということを確認(かくにん)する。
また、「かたむけるはたらきの大きさ」は、次のように求めますよ。
かたむけるはたらきの大きさ = 力の大きさ × 支点からの距離(きょり)
これらのことを意識して計算していけば、本当に簡単です。
ではさっそく、入試問題で考えていきましょう。
| 問題1 |
軽い棒に等しい間隔で図のように番号がついています。棒の太さはどこも同じで、番号5のところでばねにつるしたら水平につりあいました。ばねは20gのおもりをつるすと1cmのびます。次の問いに答えなさい。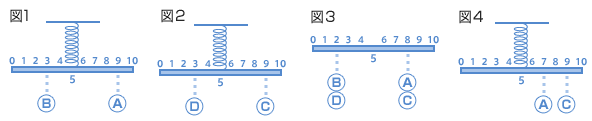 ア)20gのおもりAと重さのわからないおもりBを、図1のようにつるしたら水平につりあいました。Bの重さは何gですか。また、ばねは何cmのびますか。 重さ( )g ばね( )cm イ)重さのわからない2つのおもりC、Dを図2のようにつるし、ばねにぶらさげたらばねが4.5cmのびて、棒は水平につりあいました。おもりC、Dはそれぞれ何gですか。 おもりC( )g おもりD( )g ウ)おもりAとC、おもりBとDをつなぎ、図3のようにして水平につりあわすためには、目盛り何番のところをばねにつるせばよいですか。 エ)おもりAとCを、図4のようにつるして番号5のところでばねにつるし水平にするには、Bのおもりを何番のところにつるせばよいですか。 (同志社香里中 2003年) |
| <問題1の考え方と答え> |
| 「ばねののび」と「てんびん」が合わさった基本的な問題ですね。ここでは、棒(ぼう)の重さは考えなくてOKです。 |
| <ア)の考え方と答え> |
| Bの重さを□とすると、水平につりあっていることから次の式が成り立ちますね。 □ × 2 = 20 × 4 □ = 40(g) ばねにはAとBの重さがかかっています。 40 + 20 = 60(g) ばねは20gで1cm のびるので、60gでは |
| <イ)の考え方と答え> |
| ばねののびが4.5cmだから、おもりの重さの合計は? 20 × 4.5 = 90(g) 支点からの距離(きょり)は、(目盛り2つ分):(目盛り4つ分)= 1 : 2 です。つりあうためには、重さの比は逆比になるので、2 : 1 90(g) − 60(g) = 30(g) … おもりC |
| <ウ)の考え方と答え> |
| B + D = 40 + 60 = 100(g) A + C = 20 + 30 = 50(g) 重さの比 (B + D): (A + C) = 100 : 50 = 2 : 1 つりあうためには、支点からの距離の比は逆比になるので、1 : 2 目盛り2から目盛り8までは、目盛り6つ分あるので、それを 1 : 2 に分けると、 → 2目盛り と 4目盛り になります。 |
| <エ)の考え方と答え> |
| 右にかたむこうとするはたらきの合計は? 20 × 2 + 30 × 4 = 40 + 120 = 160 Bの重さは40g だったので、 支点からの距離(きょり)を□とすると、以下の式が成り立ちます。 40 × □ = 160 □ = 4 支点から左に4目盛りのところ いかがでしたか? 基本問題だから簡単すぎたかな? でも、応用問題もこれが基本になっています。支点がどこで、どのようにつりあっているのかをしっかり確認(かくにん)していけばだいじょうぶです。 では、次にいってみよう! |
| 問題2 |
(1) 金属の重さをはかるために、50cmのものさし、皿、200gのおもりを使って、図1のようなさおばかりをつくることにしました。ものさしの重さと皿の重さはどちらも100gです。まず図2のように、つりひもでつり下げる位置を左はしから15cm、皿をつるす位置を左はしから5cmにしたところ、おもりをつるさなくても水平になりました。このとき200gのおもりを使うと、このさおばかりは最大で何gのものをはかれますか。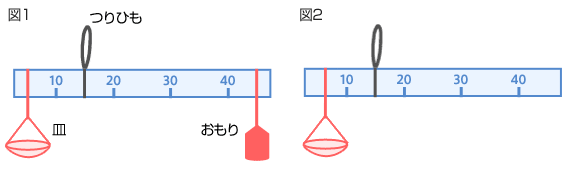 (2) あきら君が(1)のさおばかりを使って金属をはかったところ、金属が重すぎてこのさおばかりでははかれませんでした。そこで、皿の位置のみを変えて、はかれる最大の重さを1.5kgにすることにしました。このとき、皿の位置を左はしから何cmのところにすればよいですか。 (3) あきら君が(2)のさおばかりであらためて金属をはかったところ、つりひもの位置から17.4cmのところにおもりをつるしたときちょうど水平になりました。この金属の重さは何gですか。 (青山学院中 2006年 6 部分抜粋) |
| <問題2の考え方と答え> | |||
| さて、次の問題は棒(ぼう)の重さも考えるという問題です。この単元での「重さ」とは、重心一点にその重さがかかっていると考えます。 太さが均一な棒だったら、当然真ん中が「重心」となりますね。 | |||
| <問題2 (1)の考え方と答え> | |||
| ものさし 100g 皿の重さ 100g おもり 200g です。 まず確認(かくにん)しておきましょうね。 図2はどうして水平になっている(つりあっている)のかというと、 ものさしの重さ100g が、重心(両はしから25cmのところ)にすべてかかっているので、 重さ×支点からの距離(きょり)で考えることができます。 左にかたむけようとするはたらきの大きさ = 皿100g × 10cm 右にかたむけようとするはたらきの大きさ = ものさし100g × 10cm となり、 皿100g × 10 cm = ものさし 100g × 10cm で、
皿にのせるものの重さを最大まではかれるのは、おもりをいちばん右はしにつけたときですよね? 皿にのせるものの重さを□gとすると、 □ × 10 = 200 ×(ものさし50cm − 左はしから支点までの距離15cm) □ = 700 | |||
| <問題2 (2)の考え方と答え> | |||
状況(じょうきょう)を図にかいてみましょう。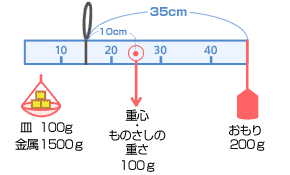 おもりとものさしの重さが右にかたむけようとしますから、右にかたむけるはたらきの大きさの合計は、 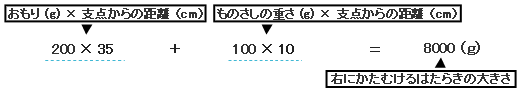 左にかたむけようとするはたらきは、皿の重さと、はかりたい1.5kg(1500g)の重さを足して、 100 + 1500 = 1600(g) となります。 あとは、皿をどれだけ支点に近づけるかですね。 左にかたむける力 × 支点からの距離 = 右にかたむけるはたらきの大きさ で、皿と支点までの距離を□cmとすると、 1600 × □ = 8000 □ = 5 → 支点から左に5cm のところ。 だから、左はしからは 15 − 5 = 10(cm) | |||
| <問題2 (3)の考え方と答え> | |||
また図をかいて整理しましょう。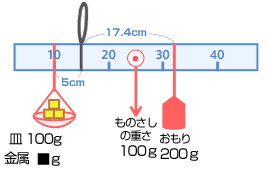 金属の重さを■とすると、以下の式が成り立ちます。 (■ + 100)× 5 = 100 × 10 + 200 × 17.4 ■= 796(g) 以上です。これも基本的な良い問題ですね。ばっちりでしょ? |
関連するおすすめの記事













![理科「てことてんびん」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/tukamu06/01.gif)








