パズルを題材に「数の面白さ」に気付く算数の授業
お気に入りに登録

東京都のAT先生の小学6年生算数の授業は、子どもたちがパズルに取り組みながら、「数の世界の面白さ」に気付いていくという内容です。どんな授業か、ご紹介しましょう。
■子どもたちの発言を引き出す
■パズルゲーム「ハノイの塔」に挑戦
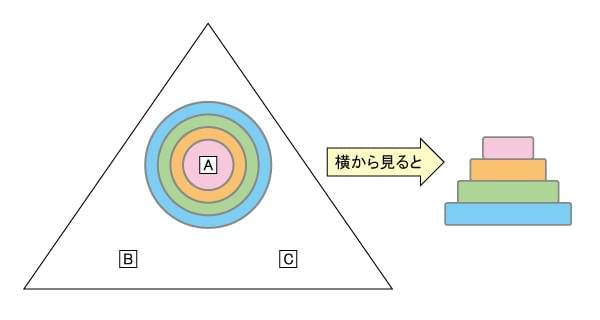
さて、今回の教材は、「ハノイの塔」と呼ばれるパズルです。下の図のように重ねた赤・青・黄色・緑の4つの円盤をA地点からBかCのいずれかの地点に引っ越しさせるというものです。
ルールは2つ。
(2)小さい円盤の上に、大きい円盤をのせてはいけない。これは、常に大きい円盤の上には、小さい円盤がのるようにしなければならない、ということです。
そして、問題は……「すべての円盤を移動させるのにかかる最少回数は何回か」ということです。ここで、先生は子どもたちに聞きます。
「予想は? 言える人は立って!」
子どもたちの頭には、円盤を動かすイメージが浮かびます。つまり、理由を言えなくても構いません。大事なのは、イメージを持つことです。あれこれ思いを巡らせることは、考えるウォーミングアップなのです。
5分以内に言えた子どもたちの予想です。
7回……2人
8回……2人
9回……2人
10回……4人
11回……1人
12回……4人
14回……1人
この後、先生は、一人ひとりに、板と4つの円盤を渡し、たっぷりと体験させます。子どもたちは、できたら先生を呼んで実演するという仕組みです。10分ほどで、「できた!」という子が現れました。先生がチェックすると、ルールもクリアー、この段階で、最少移動回数は15回となりました。すると、その子も、他の子どもたちも、もっと少ない回数でできる方法はないかと挑み続けます。ちなみに、この15回が正解なのですが……。
子どもたちは、全員が真剣です。AT先生は、この夢中になって頭を動かし、円盤を動かすイメージを培うことが大事だと考えています。それは、この後の数の不思議を考える手がかりになるからです。授業の達人と呼ばれる人の共通点のひとつが、このウォーミングアップのような考える土台づくりをとても大切にしていることだと思います。皆さんも、ぜひ試してみてください。実際やってみると、どこが難しいのかがわかってくると思います。
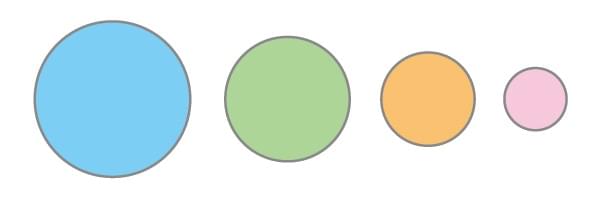
(目標は、8回目に赤が動くこと。そして、9回目で緑を赤の上に移動させることが、分かれ道です。AT先生は、「15回は、時間さえ確保すれば、試行錯誤しながらたどり着くことができる。ただ、このパズルのいいところは、試行錯誤の過程で『おやっ?』を感じている子が多いこと」だと言います。この「おやっ?」という気付きを用意できるかは、先生の力量のひとつだと思います。なぜなら、その時こそが、初めて「学びの場に立てた」ことになるからです。そして、その時こそ、パズルが算数に変わるタイミングなのです。
本当に15回か、最初にできた子が見本を見せます。と同時に、先生は下記のような表を黒板に貼りました。そして、Bに引っ越すことにして手順を確かめていきます。
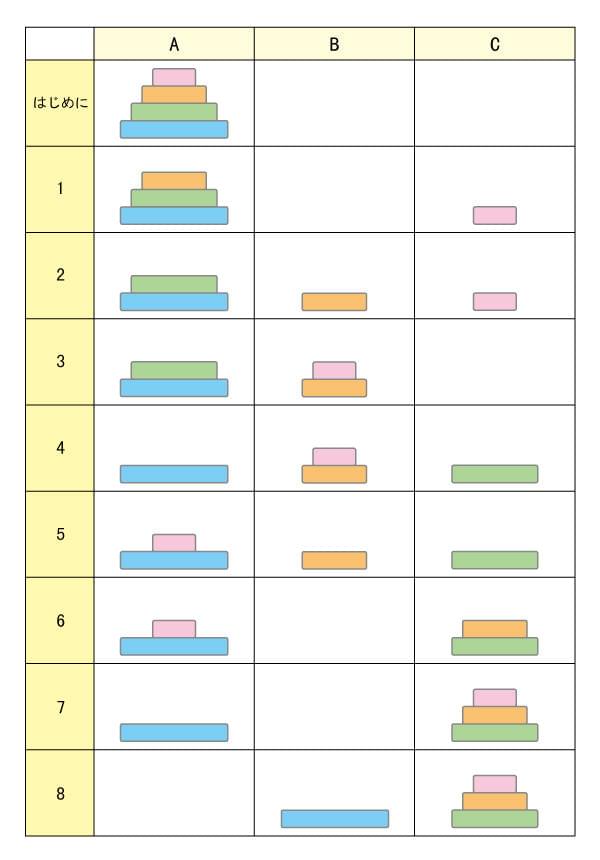
8回目赤を動かしたところで、子どもたちから「書くところがないじゃん」という声が上がります。そこで先生は尋ねました。「表を作らなきゃダメ?」子どもたち「……」。
先生は、周りの人とグループで考えるよう指示を出します。すると、「同じなんじゃない?」という声が出始めます。つまり、8回目が折り返しで、Uターンし、同じように戻ると考えたのです。確かめてみるとそのとおりです。
式で表すと……「7+1+7=15」。1は、Uターンです。続けて、先生は、「円盤が3枚だったら? 赤が動くのは何回目?」と質問します。子どもたちは、早速、円盤を動かし始めます。
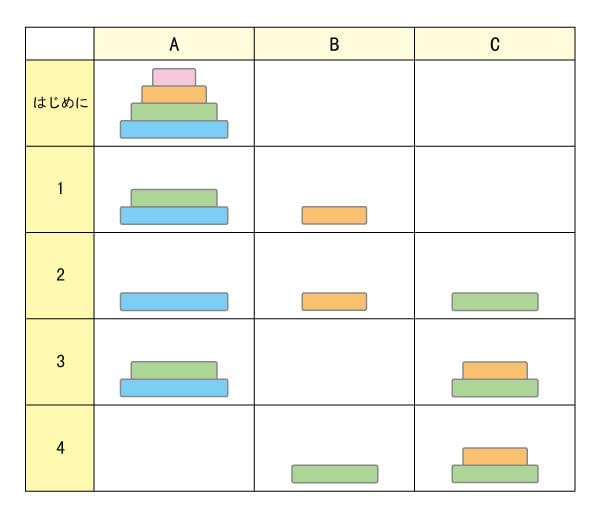
4回目でUターンとなります。つまり3回動かすと、次はUターンとなるということです。式で表すと……3+1+3=7となります。
つまり、
円盤3枚 3+1+3=7
円盤4枚 7+1+7=15
では円盤が2枚の場合は?
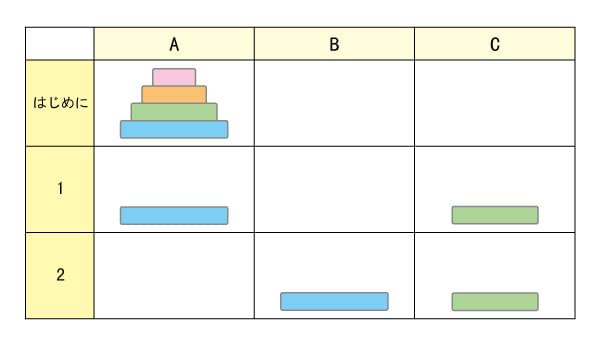
1回動かしたところでUターンとなるので、式にすると……1+1+1=3です。
円盤2枚 1+1+1=3
円盤3枚 3+1+3=7
円盤4枚 7+1+7=15
ちなみに円盤が1枚ならただ動くだけなので
円盤1枚 1 =1 です
円盤2枚 1+1+1=3
円盤3枚 3+1+3=7
円盤4枚 7+1+7=15
ちなみに円盤が1枚ならただ動くだけなので
円盤1枚 1 =1 です
円盤2枚 1+1+1=3
円盤3枚 3+1+3=7
円盤4枚 7+1+7=15
先生は、「この移動の仕組みの式を見て、気付いたことはないか?」と問いかけます。子どもたちからはさまざまな声が出ました。
・Uターンは、必ず1回
・答えの数は、奇数
・Uターンの『+1』を挟んでいる左右の数は、同じ
・左右の数は、前の答えの数と同じ
円盤1枚 1 =1
円盤2枚 1+1+1=3
円盤3枚 3+1+3=7
円盤4枚 7+1+7=15
・移動の数には、規則性がある
円盤1枚 1= 1
↓+2
円盤2枚 1+1+1=3
↓+4
円盤3枚 3+1+3=7
↓+8
円盤4枚 7+1+7=15
つまり、答えの差は、2倍になっています。
そこで、円盤5枚なら……
円盤1枚 1= 1
↓+2
円盤2枚 1+1+1=3
↓+4
円盤3枚 3+1+3=7
↓+8
円盤4枚 7+1+7=15
↓+8×2=16なので
円盤5枚 □+1+□=15+16=31となります。
したがって、□の移動の数は、(31-1)÷2=15となるのではないかと推測しました。これは、「左右の数は、前の答えの数と同じ」という子どもたちの発見した規則性にも適合していました。子どもたちは、もう確かめたくて仕方ない状態になっていました。ここで、1時間の授業は終了。子どもたちは休み時間もパズルに夢中でした。
この授業の感想を子どもたちに聞いて印象的だったのは、全員から「決まりがつかめたのは快感だった」「算数への興味が湧いた」という声を聞くことができたことです。なぜだろうと立ち止まる時こそ学びの喜びの始まり……そう改めて思いました。
(筆者:桑山裕明)
みんなが読んでる!おすすめ記事
- <目標>これから求められる資質・能力と学びとは|アクティブ・ラーニングを活用した指導と評価研究│特集
- 気にし過ぎはNG!偏差値はあくまでも「現時点の目安」
- 中学受験に役立つ読書感想文への取り組み方(2) 伝記ならこの人物がオススメ!
- 【小学生の持久走・マラソン大会のコツ】おすすめの練習方法、速く走る戦略は?
- 体格の特徴を生かす! 身長・体重を強みに変える!
- 【医師監修】寝ている時に手足がピクピク動く子ども…原因や受診の目安は?
- 言葉を使いこなす面白さを実感できる授業[こんな先生に教えてほしい]
- 血液循環と刺激が決め手! 脳の活性化で勉強の効率をアップさせる!!
- 読書感想文を通じて読解力を鍛えられる?!国語のカリスマ受験コーチがオススメする1冊と、読書とのつきあい方














![言葉を使いこなす面白さを実感できる授業[こんな先生に教えてほしい]](/img_o/kj/kyouiku/200808/20080819-3.jpg)
![地域性を生かした学びで、算数の計算法を体感させる授業[こんな先生に教えてほしい]](http://benesse.jp/common/static/kj/common/images/blog/2014/141216_p2_1.jpg)
![物語の構成をとおして「発見」の大切さに気付く国語の授業[こんな先生に教えてほしい]](http://benesse.jp/common/static/kj/common/images/blog/2016/160119_p1_1.jpg)








